Metode de analiză şi sinteză a circuitelor combinaţionale

 

Se consideră un circuit combinaţional cu n intrări şi m ieşiri. În Fig. 1 este dată o reprezentare prin schemă bloc a circuitului. Pentru acest circuit putem scrie setul de funcţii:

 

y₁=f₁(x₁,x₂,...,x_n)

y₂=f₂(x₁,x₂,...,x_n)

.........................

y_m=f_m(x₁,x₂,...,x_n)

 

unde f₁, f₂,...,f_m sunt funcţii booleene cu argumentele x₁,x₂,...,x_n

 

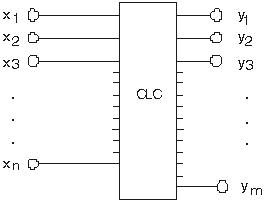
Fig. 1

1. Analiza circuitelor combinaţionale

 

În cazul problemelor de analiză se cunoaşte structura circuitului şi se cere să se stabilească valorile posibile la ieşiri pentru toate combinaţiile posibile ale valorilor semnalelor de la intrări.

Problema se soluţionează determinând expresiile funcţiilor booleene corespunzătoare semnalelor de ieşire. Pe baza acestor expresii se determină formele canonice ale funcţiilor care permit scrierea tabelei de adevăr pentru fiecare funcţie. Tabelele de adevăr conţin valorile funcţiilor pentru toate combinaţiile posibile ale variabilelor de intrare.

Pentru rezolvarea problemei de analiză se parcurg următoarele etape:

1.     Pornind de la structura circuitului se determină din aproape în aproape funcţiile corespunzătoare ieşirilor

2.     Pornind de la expresiile obţinute se obţin formele canonice ale funcţiilor corespunzătoare ieşirilor

3.     Folosind tabelul de adevăr se stabilesc valorile funcţiilor pentru toate combinaţiile posibile ale argumentelor.

Etapa neobligatorie dar de multe ori utilă din punct de vedere practic presupune obţinerea expresiilor minimale ale funcţiilor. Materializarea expresiilor minimale are drept rezultat obţinerea unui circuit echivalent cu primul dar mai economic decât primul.

 

Exemplul 1.

 

Se dă circuitul din Fig.2. realizat din 4 porţi logice. S-a notat cu y₁, y₂ şi y₃ ieşirile porţilor P₁, P₂, P₃ şi cu f₁ şi cu f₂ ieşirile porţilor P₄ şi P₅ care constituie de altfel şi ieşirile circuitului.

 

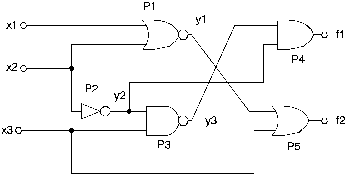
Fig. 2.

Determinarea expresiilor funcţiilor de ieşire începe parcurgând schema de la stânga la dreapta prin scrierea expresiilor la ieşirile porţilor din aproape în aproape. În cazul nostru se scriu pe rând expresiile ieşirilor notate cu y₁, y₂ şi y₃. Obţinem:

 

y₁=(x₁+x₂)’

y₂=x₂’

y₃=(x₂’.x₃)’

 

În următorul pas vom scrie expresiile pentru f₁ şi f₂ în funcţie de intrările y₁, y₂, y₃ şi x₃. Obţinem:

 

f₁=y₂.y₃

f₂=y₁+x₃

 

Înlocuind relaţiile pentru y₁, y₂ şi  y₃ se obţine pentru f₁ şi f₂ expresiile:

 

f₁=x₂’.(x₂’.x₃)’

f₂=(x₁+x₂)’+x₃

 

Folosind proprietăţile lui DeMorgan, desfăcând parantezele şi aplicând proprietăţile algebrei booleene se obţine:

 

f₁=x₂’.(x₂+x₃’)=x₂’.x₂+x₂’.x₃’=x₂’.x₃’

f₂=x₁’.x₂’+x₃

 

Se dezvoltă expresiile de mai sus pentru a se obţine formele canonice normal disjunctive (FCND):

 

f₁=(x₁+x₁’).x₂’.x₃’=x₁.x₂’.x₃’+x₁’.x₂’.x₃’=m₀+m₄

f₂=x₁’.x₂’.(x₃+x₃’)+(x₁+x₁’).(x₂+x₂’).x₃=

=x₁’.x₂’.x₃+x₁’.x₂’.x₃’+x₁.x₂.x₃+x₁.x₂’.x₃+x₁’.x₂.x₃+x₁’.x₂’.x₃=

=x₁’.x₂’.x₃+x₁’.x₂’.x₃’+x₁.x₂.x₃+x₁.x₂’.x₃+x₁’.x₂.x₃=m₀+m₁+m₃+m₅+m₇

 

Pe baza FNCD putem scrie tabelul de adevăr pentru cele două funcţii:

 

x1	x2	x3	f1	f2
0	0	0	1	1
0	0	1	0	1
0	1	0	0	0
0	1	1	0	1
1	0	0	1	0
1	0	1	0	1
1	1	0	0	0
1	1	1	0	1

 

2. Minimizarea funcţiilor booleene

 

În general, funcţionarea unui circuit combinaţional poate fi exprimată printr-un set de funcţii booleene care la rândul lor pot fi materializate prin intermediul unui circuit combinaţional. Problema de minimizare a funcţiilor booleene poate fi exprimată astfel: fiind dată o funcţie booleană f (sau un set de funcţii booleene f₁, f₂,...,f_m) să se obţină o formă a acesteia (acestora) care să satisfacă o anumită condiţie de minimalitate. Dintre cele mai utilizate criterii de minimalitate amintim:

• număr minim de apariţii a variabilelor
• număr minim de apariţii a variabilelor într-o formă normal disjunctivă a funcţiei (sumă de produse)
• număr minim de termeni într-o formă normal disjunctivă a funcţiei (sumă de produse) având în vedere că nu există altă formă normal disjunctivă cu acelaşi număr de termeni, dar cu mai puţine variabile.

 

2.1. Minimizarea FB folosind proprietăţile algebrei booleene

Ţinând cont de cel de al treilea criteriu de minimalitate, se poate obţine o sumă minimă folosind proprietăţile algebrei booleene. În general, o sumă minimă se poate obţine din forma canonică disjunctivă prin aplicarea teoremei de adiacenţă logică exprimată prin expresia x.y+x.y’=x şi proprietatea de idempotenţă exprimată prin expresia x+x=x. Teorema de adiacenţă precum şi proprietatea de idempotenţă pot fi aplicate în mod repetat până când se obţine o expresie la care aceste proprietăţi nu mai pot fi aplicate.

 

Exemplul 2. Se consideră FB f(x,y,z)=m₀+m₂+m₃+m₄+m₅+m₇=x’.y’.z’+ x’.y.z’+ x’.y.z+ x.y’.z’+ x.y’.z+ x.y.z.

 

Adăugăm încă un m₀ şi un m₇ şi apoi grupând m₀ cu m₂, m₀ cu m₄, m₃ cu m₇ şi m₅ cu m₇ se obţine:

 

f(x,y,z)=x’.z’(y+y’)+y’.z’.(x+x’) +y.z.(x’+x) +x.z.(y’+y)=x’.z’+y’.z’+y.z+x.z

 

Grupând m₀ cu m₂, m₄ cu m₅ şi m₃ cu m₇, aplicând teorema de adiacenţă şi ţinând cont de relaţia x+x’=1, obţinem:

 

f(x,y,z)=x’.z’(y+y’)+x.y’.(z’+z)+y.z.(x’+x)= x’.z’+x.y’+y.z

 

Dacă în mod similar grupăm m₂ cu m₃, m₄ cu m₀ şi m₅ cu m₇, se obţine pentru funcţia f expresia:

 

f(x,y,z)=x’.y+y’.z’+x.z

 

După cum se poate observa pentru aceeaşi funcţie am obţinut mai multe expresii reduse faţă de expresia iniţială. Dintre cele trei expresii însă numai ultimele două sunt expresii minime. Rezultă că pentru o FB se pot obţine una sau mai multe expresii minime.

 

2.2. Diagrama Veitch Karnaugh

 

Diagrama Veitch-Karnaugh (V-K) este o metodă grafică de a reprezenta într-o formă condensată tabelul de adevăr al unei FB. Poate fi folosită pentru reprezentarea FB cu un număr oricât de mare de variabile însă, în mod practic, se utilizează pentru reprezentarea FB cu până la 6 variabile.

Dacă n este numărul de variabile, diagrama V-K va avea 2ⁿ căsuţe, una pentru fiecare din cei 2ⁿ mintermi (maxtermi) ai FB deci, câte una pentru fiecare linie a tabelului de adevăr al funcţiei. Mai mult, aceste căsuţe sunt aranjate în astfel încât mintermii (maxtermii) sunt reprezentaţi într-o dispoziţie geometrică care permite evidenţierea mintermilor adiacenţi. În acest fel, minimizarea poate fi realizată prin recunoaşterea unor configuraţii în cadrul diagramei.

Liniile şi coloanele diagramei V-K sunt etichetate astfel încât combinaţia variabilelor de intrare pentru fiecare căsuţă este determinată cu uşurinţă din etichetele ataşate liniei şi coloanei corespunzătoare căsuţei.

În Fig.3 b) sunt date diagramele V-K pentru funcţii de f, g şi h având 2, 3 şi respectiv 4 variabile şi date prin tabelele de adevăr din Fig. 3 a). Numărul mic din fiecare căsuţă indică mintermul corespunzător liniei din tabelul de adevăr.

 

x	y	f			x	y	z	g			x	y	z	w	h
0	0	0	m0		0	0	0	0	m0		0	0	0	0	0	m0
0	1	1	m1		0	0	1	1	m1		0	0	0	1	1	m1
1	0	1	m2		0	1	0	1	m2		0	0	1	0	1	m2
1	1	1	m3		0	1	1	0	m3		0	0	1	1	1	m3
					1	0	0	0	m4		0	1	0	0	0	m4
					1	0	1	1	m5		0	1	0	1	0	m5
					1	1	0	0	m6		0	1	1	0	1	m6
					1	1	1	1	m7		0	1	1	1	1	m7
											1	0	0	0	0	m8
											1	0	0	1	1	m9
											1	0	1	0	0	m10
											1	0	1	1	1	m11
											1	1	0	0	0	m12
											1	1	0	1	1	m13
											1	1	1	0	1	m14
											1	1	1	1	0	m15

a)

 

			f							g										h
	x		x				yz			y							zw			z
y		0	1			x		00	01	11	10					xy		00	01	11	10
	0	00	11				0	00	11	30	21						00	00	11	31	21
	1	21	31		y		1	40	51	71	60		x				01	40	50	71	61		y
																x	11	120	131	150	141
									z								10	80	91	111	100
																			w

b)

Fig. 3.

 

2.3. Minimizarea FB folosind diagramele Veitch-Karnaugh

 

În diagrama V-K fiecare căsuţă care are un 1 corespunde unui minterm a formei canonice normal disjunctive a funcţiei. Deoarece două celule adiacente în diagramă corespund la doi mintermi care diferă între ei doar prin forma unei singure variabile, cei doi mintermi pot fi înlocuiţi printr-un singur termen folosind proprietatea de adiacenţă. În general se poate simplifica funcţia logică reprezentată prin diagrama V-K prin combinarea căsuţelor adiacente scriind termenul redus care rezultă folosind proprietatea de adiacenţă. Perechea de valori de 1 se încercuieşte indicând astfel că mintermii corespunzători se combină rezultând un singur termen.

În cazul multor funcţii booleene, procedeul de grupare a valorilor de 1 din diagrama V-K se poate extinde. În general se pot grupa 2ⁱ căsuţe conţinând valori de 1 rezultând un termen care conţine n-i variabile, unde n este numărul de variabile ale funcţiei.

Regula prin care se determină cum pot fi grupate căsuţele conţinând valori de 1 este următoarea:

- o mulţime de 2ⁱ celule pot fi grupate dacă există i variabile ale funcţiei booleene care iau toate cele 2ⁱ combinaţii posibile în acea mulţime de căsuţe în timp ce celelalte n-i variabile au aceeaşi valoare pentru aceeaşi mulţime de căsuţe. Termenul corespunzător grupării va conţine cele n-i variabile în care variabila este în formă normală dacă ea apare ca 1 pentru toate căsuţele grupării şi în forma negată dacă ea apare ca 0 pentru toate căsuţele grupării.

Din punct de vedere grafic, regula de mai sus ne spune că putem încercui mulţimi dreptunghiulare având 2ⁱ valori de 1, prin aceasta înţelegând şi mulţimile dreptunghiulare obţinute dacă muchiile opuse diagramei ar fi unite.

Se pot determina variabilele şi forma pe care acestea o au în termenul rezultant:

·       dacă o încercuire acoperă căsuţe în care variabila este 0 atunci variabila apare în termenul rezultant în forma negată

·       dacă o încercuire acoperă căsuţe în care variabila este 1, atunci variabila apare în termenul rezultant în forma normală.

·       dacă o încercuire acoperă atât căsuţe în care variabila este 0 dar şi căsuţe în care variabila este 1, atunci acea variabilă nu mai apare în termenul rezultant.

 

În Fig.4 sunt date grupările posibile pentru funcţiile g şi h prezentate anterior şi termenii rezultanţi corespunzători.

 

 

 

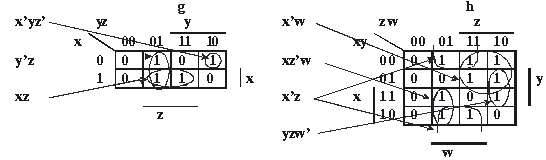
Fig. 4.

 

Conform Fig.4 putem scrie:

 

g(x,y,z)=xz+y’z+x’yz’

h(x,y,z,w)=x’w+xz’w+x’z+yzw’

 

Teorema implicanţilor primi afirmă că pentru o funcţie booleană, o expresie sub forma normală (sumă de produse) minimală este o sumă de implicanţi primi ai funcţiei. Rezultă că pentru a obţine o expresie minimală a funcţiei nu va trebui să luăm în considerare termenii care nu sunt implicanţi primi.

În cadrul diagramei V-K, un implicant prim este reprezentat printr-o încercuire rectangulară de valori de 1 (conform regulii prezentate anterior) care dacă încercăm să o mărim (acoperind de două ori mai multe căsuţe) va cuprinde şi valori de 0.

O expresie minimală se va obţine astfel prin alegerea încercuirilor cele mai mari şi astfel încât fiecare valoare de 1 să fie cuprinsă în cât mai puţine încercuiri (Fig. 5).

 

 

 

 

 

 

 

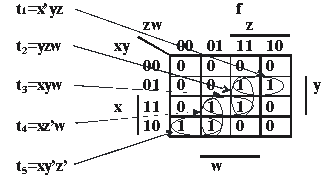
Fig.5

În Fig. 5 o expresie a funcţiei f reprezentată sub forma unei diagrame V-K se obţine ca suma:

 

f(x,y,z)=t₁+t₂+t₃+t₄+t₅

 

însă forma minimală se obţine ca suma:

 

f(x,y,z)=t₁+t₃+t₅= x’yz+ xyw+ xy’z’

 

3. Sinteza circuitelor combinaţionale

 

Problema de sinteză a circuitelor combinaţionale se defineşte în modul următor: cunoscând modul de funcţionare a circuitului combinaţional exprimat prin valorile semnalelor de ieşire corespunzătoare diferitelor combinaţii ale variabilelor de intrare, se cere să se stabilească structura circuitului.

Ţinând cont de această formulare, rezultă că rezolvarea problemei de sinteză presupune parcurgerea a două etape:

1. sinteza abstractă, care constă în stabilirea expresiilor funcţiilor booleene care corespund condiţiilor impuse între semnalele de ieşire şi de intrare. Pentru ca circuitul realizat să fie cât mai simplu şi deci mai economic, se caută expresiile minime ale funcţiilor. Din punct de vedere matematic, problemele de sinteză presupun minimizarea funcţiilor booleene în sistemul de funcţii elementare alese din considerente practice;
2. sinteza structurală, care constă în determinarea structurii fizice a circuitului sintetizat. Sinteza structurală se face în funcţie de tipul circuitelor logice elementare (module) şi de numărul de intrări ale acestora, de semnalele disponibile în diferite puncte ale sistemului etc.

Algoritmul sintezei circuitelor combinaţionale va fi:

1. Din condiţiile problemei se stabilesc corespondenţele între combinaţiile semnalelor de intrare şi ieşire folosind tabelul de adevăr, diagrama V-K etc.
2. Se realizează minimizarea funcţiilor booleene care rezultă din etapa precedentă
3. Se implementează daca este cazul cu funcţiile elementare impuse de realizarea practică
4. Se stabileşte logigrama plecând de la forma minimă obţinută pentru funcţiile de ieşire în pasul al treilea
5. Se analizează circuitul obţinut pentru a vedea dacă corespunde condiţiilor impuse iniţial (etapă facultativă).

 

Exemplul 3.

Să se realizeze circuitul cu trei intrări şi cu o ieşire pentru care ieşirea este egală cu 1 dacă cel puţin două intrări au valoarea 1.

 

Din descrierea problemei rezultă că funcţionarea circuitului poate fi descrisă cu ajutorul unei funcţii booleene cu trei intrări. Să le numim pe acestea x, y şi z şi vom nota cu f ieşirea circuitului. Vom completa tabelul de adevăr al funcţie pe baza datelor din problemă punând valoare 1 pentru liniile care au cel puţin două valori de 1 şi 0 în rest:

 

x	y	z	f
0	0	0	0
0	0	1	0
0	1	0	0
0	1	1	1
1	0	0	0
1	0	1	1
1	1	0	1
1	1	1	1

 

În etapa următoare căutăm să simplificăm funcţia f folosind diagrama V-K pe care o completăm pe baza tabelului de adevăr şi realizăm grupările din figură:

 

 

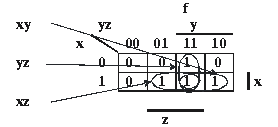
Putem scrie astfel expresia simplificată a funcţiei sub forma:

 

f(x,y,z)=xy+xz+yz

 

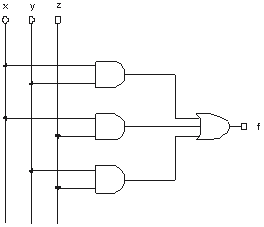
Folosind porţi logice de tip SI şi SAU obţinem schema logică următoare: