Metode de analiză şi sinteză a circuitelor secvenţiale

În Fig. 1 este dată o reprezentarea generală prin schemă bloc a unui circuit secvenţial. Funcţionarea acestui circuit poate fi descrisă prin următorul set de ecuaţii:

z₁=g₁(x₁,x₂,...,x_n,y₁,y₂,...,y_k)

z₂=g₂(x₁,x₂,...,x_n,y₁,y₂,...,y_k)

.........................

z_m=g_m(x₁,x₂,...,x_n,y₁,y₂,...,y_k)

pentru ieşiri şi:

Y₁=f₁(x₁,x₂,...,x_n,y₁,y₂,...,y_k)

Y₂=f₂(x₁,x₂,...,x_n,y₁,y₂,...,y_k)

.........................

Y_k=f_k(x₁,x₂,...,x_n,y₁,y₂,...,y_k)

pentru semnalele secundare care definesc starea următoare a circuitului, unde g₁, g₂,...,g_m şi f₁, f₂,...,f_k sunt funcţii booleene cu argumentele x₁,x₂,...,x_n,y₁,y₂,...,y_k. Materializarea funcţiilor f_i si g_i formează un circuit logic combinaţional reprezentat prin blocul CLC. Blocul M conţine elementele de memorare care pot fi circuite basculante bistabile de tip R-S, J-K, D sau T sau, simple elemente de întârziere.

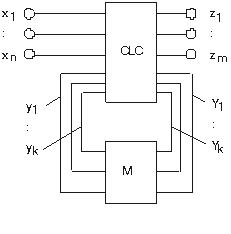
Fig. 1

1. Analiza circuitelor secvenţiale

Problema de analiză a circuitelor secvenţiale se defineşte astfel: cunoscând structura circuitului secvenţial se cere evoluţia semnalelor de ieşire pentru anumite evoluţii (secvenţe) ale semnalelor de intrare.

O condiţie necesară pentru rezolvarea problemei de analiză a circuitelor secvenţiale o constituie cunoaşterea stării iniţiale a circuitului analizat.

Atât pentru circuitele sincrone cât şi pentru cele asincrone, analiza presupune parcurgerea următoarelor etape:

1. Pornind de la structura circuitului se determină părţile combinaţionale şi cele de memorie şi se definesc semnalele de intrare, de ieşire şi semnalele secundare (de stare)

2. Se stabilesc expresiile funcţiilor booleene ale ieşirilor din partea combinaţională. Funcţiile stabilite se pun în forma canonică

3. Corespunzător combinaţiilor variabilelor de stare se realizează codificarea stărilor şi se definesc stările circuitului

4. Se construieşte tabelul stărilor şi/sau graful de tranziţie a circuitului

5. Pentru evoluţia semnalelor de intrare şi starea iniţială impusă, folosindu-se graful sau tabelul de tranziţie, se stabileşte evoluţia semnalelor la ieşire.

Etapa neobligatorie dar de multe ori utilă din punct de vedere practic presupune obţinerea expresiilor minimale ale funcţiilor de ieşire şi de tranziţie. Materializarea expresiilor minimale are drept rezultat obţinerea unui circuit echivalent cu primul dar mai economic decât primul.

Exemplul 1.

Se dă circuitul din Fig.2. realizat din 9 porţi logice şi două CBB tip D.

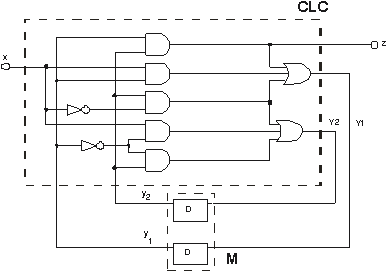
Fig. 2.

Observându-se că în cadrul circuitului există legături de reacţie, rezultă că circuitul este unul secvenţial. Ca urmare, se urmăresc etapele de analiză a unui circuit secvenţial.

1. Pe schemă s-a pus în evidenţă partea combinaţională (CLC) şi partea de memorie (M). Circuitul are o bornă de intrare (x), una de ieşire (z) şi două bucle de reacţie cu variabilele secundare y₁ şi y₂.

2. Expresiile funcţiilor de ieşire a părţii combinaţionale se determină în mod similar ca în cazul analizei circuitelor combinaţionale. Rezultă următoarele expresii:

z=y₁y₂

Y₁=y₁y₂+xy₁+x’y₂

Y₂=xy₁’+x’y₂+y₁’y₂

Prin dezvoltare se obţin formele canonice ale funcţiilor:

z=xy₁y₂+x’y₁y₂

Y₁=xy₁y₂+ x’y₁y₂+xy₁y₂’+x’y₁’y₂

Y₂=xy₁’y₂+ xy₁’y₂’+x’y₁y₂+x’y₁’y₂

Obţinerea formelor canonice poate fi realizată şi direct pe diagrama Veitch-Karnaugh (V-K). În Fig. 3, funcţiile y₁ şi y₂ sunt reprezentate pe aceeaşi diagramă şi separat este reprezentată funcţia z.

			Y1-Y2							z
	y1y2			y1				y1y2			y1
x		00	01	11	10		x		00	01	11	10
	0	00	11	11	00			0	0	0	1	0
	1	01	01	10	10	x		1	0	0	1	0	x
			y2							y2

Fig. 3

3. Circuitul studiat are două variabile de stare. Ca urmare, cele 4 combinaţii posibile ale valorilor acestora definesc stările circuitului. Putem scrie următoarea codificare:

y1	y2		sk
0	0	->	s0
0	1	->	s1
1	0	->	s2
1	1	->	s3

Conform acestei codificări şi a condiţiilor problemei, starea iniţială a circuitului studiat este starea s₀.

4. Având în vedere codificarea realizată şi diagrama din Fig. 3, se poate stabili imediat tabelul stărilor. Tabelul corespunde unei reprezentări prin tabel a automatelor Moore.

În tabel s-au evidenţiat stările stabile adică, stările pentru care stare prezentă şi starea următoare sunt identice.

x sk	0	1	z
s0	s0	s1	0
s1	s3	s1	0
s2	s0	s2	0
s3	s3	s2	1

Pe baza acestui tabel se poate stabili imediat graful de tranziţie al circuitului care este dat în Fig. 4. Starea iniţială este reprezentată printr-un cerc cu linie dublă.

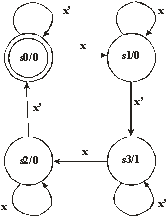
Fig.4

3. Sinteza circuitelor secvenţiale

Problema de sinteză a circuitelor combinaţionale se defineşte în modul următor: cunoscând modul de funcţionare a circuitului secvenţial exprimat prin evoluţia semnalelor de intrare respectiv a celor de ieşire (secvenţele de intrare respectiv cele de ieşire), se cere să se stabilească structura circuitului.

Ţinând cont de această formulare, rezultă că rezolvarea problemei de sinteză presupune parcurgerea etapelor:

1. Se construieşte tabelul tranziţiilor şi ieşirilor din specificaţia dată sub formă de descriere verbală

2. Se minimizează numărul stărilor

3. Se realizează codificarea stărilor

4. Se substituie combinaţia variabilelor de stare în tabelul stărilor şi ieşirilor pentru a crea tabelul tranziţiilor şi stărilor

5. Se alege tipul de celule de memorie folosite (tip R-S, J-K, D, T)

6. Se construieşte tabelul de excitaţie care indică valorile excitaţiilor necesare pentru a obţine starea următoare dorită pentru fiecare combinaţie stare actuală-intrare

7. Se obţin expresiile funcţiilor de excitaţie

8. Se obţin expresiile funcţiilor de ieşire

9. Se trasează schema logică a circuitului care materializează funcţiile de excitaţie şi cele de ieşire la care se adaugă şi celulele de memorie corespunzătoare.

Dintre etapele prezentate mai sus, prima este cea mai dificilă şi afectată de erori. Parcurgerea ei cu succes depinde foarte mult de experienţa şi abilităţile proiectantului. Fiecare din celelalte etape poate fi parcurse în mod sistematic manual sau folosind programe pe calculator specializate.

În ceea ce priveşte prima etapă, se recomandă construirea unui tabel de tranziţii primar unde să fie o singură stare stabilă pe fiecare linie a tabelului. Fiind doar o singură stare stabilă pe fiecare linie a tabelului, ieşirea poate fi considerată ca depinzând numai de starea curentă. În acest fel este posibil să se introducă stări suplimentare care însă pot fi eliminate mai târziu în etapa de minimizare a stărilor.

Exemplul 2

Să se realizeze circuitul secvenţial care are 2 intrări, a şi b, o ieşire z care iniţial este 0. Secvenţa semnalelor de intrare 10, 11, 01 face ca ieşirea să devină 1. Următoarea modificare a intrării duce la trecerea ieşirii în 0. Nici o altă secvenţă a semnalelor de intrare nu mai produce 1 la ieşire.

Etapa 1.

Se realizează tabelul de tranziţii primar. Acesta are următorul cap de tabel:

Semnificaţia stării	Numele stării	Intrări				Ieşire
		00	01	11	10

Tabelul de tranziţii primar se completează apoi linie cu linie pe baza descrierii verbale a funcţionării circuitului.

Se consideră că funcţionarea circuitului începe dintr-o stare care de obicei este starea în care se află sistemul după ce a fost cuplat la sursa de alimentare. Această stare o vom numi starea iniţială şi o vom nota cu SInit.

Apoi pentru fiecare combinaţie a variabilelor de intrare vom analiza evoluţia circuitului. Conform descrierii funcţionării circuitului, o singură secvenţă a semnalelor de intrare poate duce la activarea ieşirii şi prima combinaţie din această secvenţă este 10. Rezultă ca pentru combinaţiile 00, 01, şi 11 circuitul va rămâne în starea în care se află iar pentru combinaţia 10 el va trece într-o stare nouă. Aceasta este starea în care s-a detectat prima combinaţie din secvenţă aşa încât o vom numi Detect1. Pentru starea iniţială ieşirea va fi 0.

Semnificaţia stării	Numele stării	Intrări				Ieşire
		00	01	11	10
Starea iniţială	SInit	SInit	SInit	SInit	Detect1	0

Noua stare Detect1 se adaugă tabelului primar prin adăugarea unei linii suplimentare şi procesul prezentat mai sus se reia.

Semnificaţia stării	Numele stării	Intrări				Ieşire
		00	01	11	10
Starea iniţială	SInit	SInit	SInit	SInit	Detect1	0
S-a detectat prima combinaţie din secvenţă	Detect1

Următoarea combinaţie din secvenţa care duce la activarea ieşirii z este 11. Asta înseamnă că dacă, aflându-ne în starea Detect1, la intrare se aplică combinaţiile 00 sau 01, secvenţa rezultată va fi una din (10, 00) sau (10, 01) care conform specificaţiilor nu vor putea duce la validarea ieşirii z. Ca urmare, în aceste două cazuri circuitul va trebui să se întoarcă în starea iniţială pentru a relua procesul de detecţie a secvenţei corecte. În cazul în care combinaţia la intrare este 10, rezultă că aceasta a rămas neschimbată aşa încât circuitul va rămâne în continuare în starea Detect1 aşteptând modificarea secvenţei de intrare. Circuitul va trece într-o stare nouă doar dacă la intrare se aplică combinaţia 11. Această nouă stare corespunde detecţiei celei de a doua combinaţie din secvenţa care activează ieşirea z aşa încât o vom numi Detect2. Ieşirea circuitului rămâne în continuare 0. Tabelul primar va arăta astfel:

Semnificaţia stării	Numele stării	Intrări (ab)				Ieşire
		00	01	11	10
Starea iniţială	SInit	SInit	SInit	SInit	Detect1	0
S-a detectat prima combinaţie din secvenţă	Detect1	SInit	SInit	Detect2	Detect1	0
S-a detectat a doua combinaţie din secvenţă	Detect2

Raţionând în mod similar rezultă că pentru combinaţiile 00 şi 10 circuitul revine în starea iniţială, pentru combinaţia 11 circuitul rămâne în starea Detect2 iar pentru combinaţia 01 circuitul trece într-o stare nouă. Aceasta este starea în care a fost detectată şi cea de a treia combinaţie din secvenţă de activare a ieşirii z şi ca urmare aceasta va fi activată. Noua stare o vom numi Detect3. Din această stare circuitul revine în starea iniţială la oricare din combinaţiile diferite de ultima recepţionată, adică 01.

Cum în această ultimă etapă nu au apărut stări noi, rezultă că procesul determinării tabelului de tranziţie primar s-a încheiat. Forma finală a acestuia este:

Semnificaţia stării	Numele stării	Intrări				Ieşire
		00	01	11	10
Starea iniţială	SInit	SInit	SInit	SInit	Detect1	0
S-a detectat prima combinaţie din secvenţă	Detect1	SInit	SInit	Detect2	Detect1	0
S-a detectat a doua combinaţie din secvenţă	Detect2	SInit	Detect3	Detect2	SInit	0
S-a detectat a treia combinaţie din secvenţă	Detect3	SInit	Detect3	SInit	SInit	1

Din tabelul de tranziţie primar se obţine imediat tabelul de tranziţie al circuitului:

Numele stării	Intrări (ab)				Ieşire z
	00	01	11	10
SInit	SInit	SInit	SInit	Detect1	0
Detect1	SInit	SInit	Detect2	Detect1	0
Detect2	SInit	Detect3	Detect2	SInit	0
Detect3	SInit	Detect3	SInit	SInit	1

Etapa 2.

În această etapă se urmăreşte eliminarea stărilor suplimentare introduse în procesul de determinare a tabelului de tranziţie a circuitului. Diverse metode de reducere a stărilor suplimentare pot fi găsite în manulalele de specialitate.

Etapa 3.

Stările automatului sunt realizate prin itermediul variabilelor de stare. Cum aceste variabile pot lua doar două valori rezultă că pentru n stări vom avea nevoie de cel puţin m variabile binare, unde 2^m³n. În cazul nostru n=4 aşa încât vom utiliza 2 variabile de stare pe care le vom nota cu y₁ şi y₂. Vom alege următoarea codificare a stărilor:

SInit -> y₁=0 y₂=0

Detect1 -> y₁=0 y₂=1

Detect2 -> y₁=1 y₂=1

Detect3 -> y₁=1 y₂=0

În general există n! posibilităţi de codificare a celor n stări.

Etapa 4.

Înlocuind codurile de mai sus în tabelul de tranziţie obţinem:

ab y1y2	00	01	11	10	z
00	00	00	00	01	0
01	00	00	11	01	0
11	00	10	11	00	0
10	00	10	00	00	1

Din acest tabel putem obţine diagramele Veitch-Karnaugh (V-K) corespunzătoare funcţiilor de stare Y₁ şi Y₂ corespunzătoare variabilelor de stare y₁ şi y₂ precum şi funcţiei de ieşire z. Utilizând aceste diagrame putem minimiza aceste funcţii.

Grupând valorile de 1 se obţin următoarele expresii:

Y₁=a’by₁+aby₂

Y₂=ab’y₁’+aby₂

z=y₁y₂’

Etapa 5.

În această etapă se alege tipul de celule de memorie folosite (tip R-S, J-K, D, T).

Etapa 6.

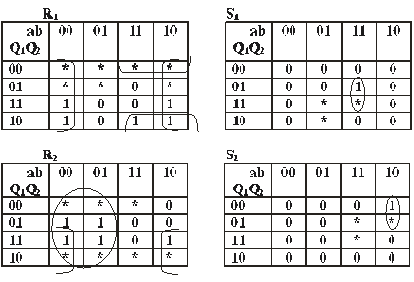
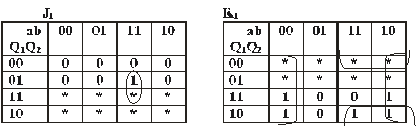
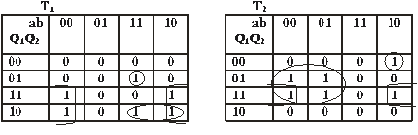
Pentru tipul de memorie aleasă se construieşte tabelul de excitaţie care indică valorile excitaţiilor ce trebuiesc aplicate intrărilor memoriilor pentru a obţine starea următoare dorită pentru fiecare combinaţie stare actuală-intrare. Aplicând regulile din Anexa 1 se obţin următoarele tabele de excitaţii:

Celule de memorie tip D

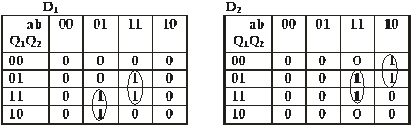
Celule de memorie tip R-S

Celule de memorie tip J-K

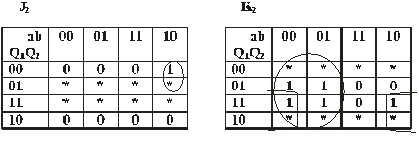
Celule de memorie tip T

Etapa 7.

Pe baza diagramei V-K şi a tabelelor de excitaţie celulelor de memorie folosite se obţin expresiile funcţiilor de excitaţie.

Celule de memorie tip D

D₁=a’.b.Q₁+a.b.Q₂

D₂=a.b’.Q₁’+a.b.Q₂

Celule de memorie tip R-S

R₁=b’+a.Q₂’

S₁=a.b.Q₂

R₂=a’+b’.Q₁

S₂=a.b’.Q₁’

Celule de memorie tip J-K

J₁=a.b.Q₂

K₁=b’.Q₁+a.Q₂’

J₂=a.b’.Q₁’

K₂=a’.b’+b’.Q₁

Celule de memorie tip T

T₁=b’.Q₁+a.Q₁.Q₂’+a.b.Q₁’.Q₂

T2=a’.Q₂+b’.Q₁.Q₂+a.b’.Q₁’.Q₂’

Etapa 8.

Pe baza tabelului de tranziţie se obţine expresia funcţiei de ieşire. Pentru toate cazurile, funcţia de ieşire depinde numai de starea circuitului şi conform diagramei V-K de mai jos va avea expresia:

z= Q₁.Q₂’

Etapa 9.

Pe baza ecuaţiilor determinate în etapele 8 şi 9 se trasează schema logică a circuitului care materializează funcţiile de excitaţie şi cele de ieşire la care se adaugă şi celulele de memorie corespunzătoare. Schemele logice sunt date mai jos pentru fiecare tip de celulă de memorie.

Celule tip D

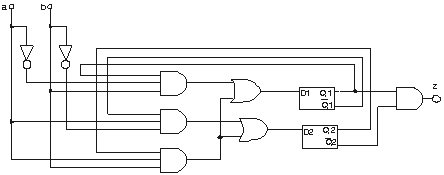
Celule tip RS

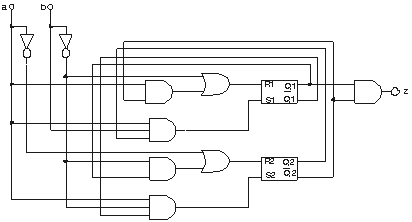
Celule tip JK

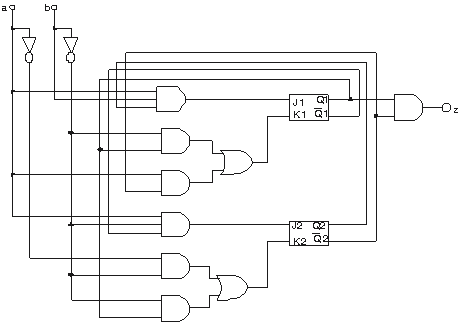
Celule tip T

După cum se observă, în funcţie de tipul de celule de memorie alese, numărul şi tipul porţilor logice necesare pentru materializarea funcţiilor de excitaţie şi a funcţiei de ieşire diferă.

Anexa 1

Reguli privind determinarea expresiilor excitaţiei CBB din diagrama stărilor următoare.

		Qn=0		Qn=1		Reguli
Tip	Intrare	Qn+1=0	Qn+1=1	Qn+1=0	Qn+1=1	Qn=0	Qn=1
D		0	1	0	1	nu se schimbă	nu se schimbă
T	EN	0	1	1	0	nu se schimbă	complementează
S-R	S	0	1	0	*	nu se schimbă	înlocuieşte 1 cu *
	R	*	0	1	0	schimbă 0 cu *	complementează
J-K	J	0	1	*	*	nu se schimbă	completează cu *
	K	*	*	1	0	completează cu *	complementează

Observaţii

1. * semnifică valori indiferente

2. Întotdeauna se copie mai întâi valorile indiferente din diagrama stărilor următoare în diagrama intrărilor

3. Pentru diagrama lui S, rândul de căsuţe pentru care Q_n=1 şi pentru diagrama R, rândul de căsuţe pentru care Q_n=0 se completează căsuţele rămase libere cu valori de 0.

Exemplul 3. Pentru diagrama de mai jos,

				Qn*1
	xy			x
Qn		00	01	11	10
	0	0	1	0	1
	1	1	0	0	*	Qn
			y

se obţin următoarele diagrame ale funcţiilor de excitaţie:

				D							T
	xy			x				xy			x
Qn		00	01	11	10		Qn		00	01	11	10
	0	0	1	0	1			0	0	1	0	1
	1	1	0	0	*	Qn		1	0	1	1	*	Qn
			y							y

				R							S
	xy			x				xy			x
Qn		00	01	11	10		Qn		00	01	11	10
	0	*	0	*	0			0	0	1	0	1
	1	0	1	1	*	Qn		1	*	0	0	*	Qn
			y							y

				J							K
	xy			x				xy			x
Qn		00	01	11	10		Qn		00	01	11	10
	0	0	1	0	1			0	*	*	*	*
	1	*	*	*	*	Qn		1	0	1	1	*	Qn
			y							y