Metode
numerice - Aplicatii
Lucrarea
11.
Integrarea numerica cu metode de cuadratura: metoda trapezelor, metoda Simpson,
metoda Romberg cu extrapolare Richardson
Tema A - Metoda trapezelor
Tema B - Metoda Simpson
Tema C - Metoda Romberg cu extrapolare Richardson
O problema de
integrare numerica urmareste determinarea aproximativa, pe cale numerica, a valorii unei integrale definite. In analiza
matematica problema este definita cat se
poate de concis, folosind notiunea de
primitiva :daca pentru functia f(x)
– continua in intervalul [a,b] – se cunoaste primitiva F(x)
, integrala definita a acestei functii intre limitele a si
b se calculeaza cu formula
Newton-Leibnitz:
![]()
In
practica exista insa numeroase situatii in care primitiva F(x) fie are o expresie complicata, fie – pur si simplu - nu
poate fi determinata pe cai elementare, analitice. Totodata, este posibil ca
functia f(x) sa fie data sub forma
tabelara, situatie in care insasi notiunea de primitiva isi pierde sensul. In
asemenea cazuri, calculul integralei definite cu relatia anterioara
nu mai este posibil, fiind necesara aplicarea unor procedee de integrare
numerica, numite si metode de cuadratura.
In principiu toate metodele de
cuadratura numerica calculeaza o valoare aproximativa a integralei definite
pornind de la un numar finit de valori cunoscute ale functiei integrand f(x). Majoritatea metodelor de
cuadratura aproximeaza functia integrand printr-un polinom si determina
valoarea integralei definite aplicand formula Newton-Leibnitz polinomului de
aproximare fie pe intregul interval [a,b],
fie pe subdiviziuni ale acestuia.
Tema
A - Metoda trapezelor
.
In acest caz, pe intervalul [a,b] se
definesc numai doua puncte de diviziune, care coincid cu extremitatile
intervalului: x1=a si x2=b, iar integrala ![]() se calculeaza
aproximativ cu relatia:
se calculeaza
aproximativ cu relatia:
![]()
care
reprezinta formula trapezului. Acestei
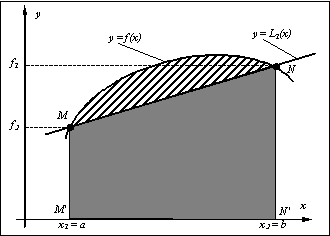
formule i se poate asocia o interpretare geometrica simpla (vezi figura).
Deoarece polinomul de interpolare este de grad n=1 curba functiei integrand y(x)
este aproximata cu dreapta ce trece prin punctele M(x1,f1) si N(x2,f2), iar integrala definita este
aproximata prin aria trapezului MM’N'N,
conform relatiei de definitie
 .
.
Eroarea de
aproximare ce se produce la folosirea formulei trapezului corespunde ariei
hasurate din figura, iar cantitativ calculeaza astfel:
![]()
unde xÎ[a,b] care reprezinta o medie a punctelor xkÎ[xk , xk+1], astfel incat: ![]()
Algoritmul 1 – Metoda trapezelor
1.
Definirea
functiei integrand f(x) fie sub forma analitica, fie sub forma
tabelara; in primul caz se indica limitele de integrare a si b, respective
numarul subintervalelor elementare, n ; in cel de-al doilea caz se
precizeaza perechile [x(i), f(x(i))],
i=1..n+1, cu x(1)=a si x(n+1)=b;
2.
Calculul
lungimii subintervalului elementar: h=(b-a)/n;
3.
Calculul
aproximativ al integralei:
![]()
4.
Afisarea
valorii aproximative a integralei I
Spre deosebire de metoda trapezelor, care
foloseste un polinom de interpolare liniar, metoda Simpson foloseste polinoame
de interpolare parabolice, de gradul doi. Din acest motiv, este de asteptat ca
in cazul unor functii integrand suficient de netede precizia acestei metode sa
fie superioara. Intervalul [a,b]
contine trei puncte de diviziune: doua dintre acestea coincid cu extremitatile x1=a, x3=b, iar al
treilea realizeaza injumatatirea intervalului x2=(a+b)/2.
Valoarea
aproximativa a integralei ![]() se calculeaza in acest
caz cu formula Simpson:
se calculeaza in acest
caz cu formula Simpson:
![]()
Datorita
simetriei formulei, eroare de aproximare calculata prin particularizarea
relatiei (7.63) pentru n=2 va rezulta
nula. Nu trebuie sa intelegem de aici ca formula Simpson ar fi precisa
intotdeauna. Rezultatul pe care il furnizeaza este exact numai cand functia
integrand este un polinom de grad maxim trei, inclusiv.
Formula erorii este:
![]()
Algoritmul
2 – Metoda Simpson
1.
Definirea
functiei integrand f(x) fie sub forma analitica, fie sub forma
tabelara; in primul caz se indica limitele de integrare a si b, respective numarul subintervalelor elementare, n=2p ; in cel de-al doilea caz se
precizeaza perechile [x(i), f(x(i))],
i=1..n+1, cu x(1)=a si x(n+1)=b;
2.
Calculul
lungimii subintervalului elementar: h=(b-a)/(2p+1);
3.
Calculul
aproximativ al integralei:
![]()
4.
Afisarea
valorii aproximative a integralei I
Tema C - Metoda Romberg cu extrapolare Richardson
Metoda Romberg urmareste imbunatatirea
preciziei formulelor de cuadratura numerica prin aplicarea repetata a uneia din
formule (formula trapezelor, formula Simpson, etc.) insotita de injumatatirea
pasului h, deci dublarea numarului de
subintervale de lucru. Din acest motiv, atunci cand functia obiectiv este
definita sub forma tabelara, metoda Romberg poate fi aplicata numai daca
numarul punctelor prin care este definite functia conduce la un numar de
subintervale egal cu o putere a lui 2. Dublarea numarului de intervale de lucru
este de asteptat sa duca la cresterea preciziei.
Se va ilustra aplicarea metodei Romberg in
cazul formulei trapezelor. Se va calcula integrala ![]() folosind formula
folosind formula
![]()
Formula metodei Romberg se va stabili prin
inductie, utilizand n=2k
subintervale. Initial, se considera numai doua puncte: a=x1 si b=x2.
in acest caz, h=b-a, n=1, k=0. Rezulta:
![]()
Se injumatateste pasul h, lucrand cu trei puncte: a=x1,
x2=x1+h,b=x3; atunci h=(b-a)/2, n=2, k=1. Se obtine:
![]()
In general, dupa k-1 injumatatiri ale pasului h
se poate scrie
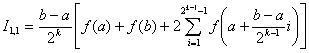
Sirul astfel construit tinde catre valoarea
exacta a integralei ce se calculeaza. Se calculeaza repetat integrale de forma I1,k, pana cand abaterea
intre doua aproximatii successive |I1,k,
I1,k+1 | scade sub o anumita valoare prag considerata ca limita
de precizie.
Cresterea vitezei de convergenta a metodei
Romberg este posibila daca acesteia i se asociaza procedura de extrapolare
Richardson. Aceasta procedura foloseste doua valori successive din sirul
aproximatiilor Romberg, I1,k
si I1,k+1 pentru a calcula
o alta aproximatie I2,k,
mai precisa, cu relatia:
![]() ,
,
sau, in general:
![]()
Sirurile
generate pe baza acestei recurente formeaza un tablou cu K
linii si tot atatea coloane. Prima linie
I1,1…….,I1,K
reprezinta sirul Romberg construit pe baza formulei generalizate a
trapezului. Pentru restul liniilor,
numarul elementelor din sirurile
Romberg se micsoreaza treptat, astfel incat pentru o linie j sunt definite K-j+1 elemente:
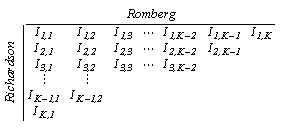
Fiecare coloana k a acestui tabel reprezinta un sir Richardson. La limita, pentru k ® ¥, cea ce este
totuna cu un pas h ® 0, sirurile Romberg / Richardson tind spre valoarea
exacta a integralei care se calculeaza. Se poate demonstra ca , datorita
ordinului crescator al formulei de cuadratura folosite, convergenta sirului
Richardson este mult mai rapida. Datorita acestei proprietati, in practica nu
se calculeaza toate elementele tabloului, ci se aplica un algoritm iterativ
conform celui descris in continuare.
Algoritmul
3 – Metoda Romberg cu extrapolare Richardson
1.
Definirea functiei integrand f(x) si a limitelor de integrare [a,b]. Functia f(x) se
defineste sub forma analitica sau tabelara. In ultimul caz tabelul de definitie
va contine M=2K-1+1 puncte
(xk, fk), k=1,...,M.
2.
Definirea parametrilor de iterare: precizia Eps si numarul maxim de iteratii Nmax.
3.
Initializarea procesului iterativ pentru sirul Romberg
de ordin doi:
3.1.
Primul element din sir: I1,1;
3.2.
Contor: K ¬ 2;
4.
Procesul iterativ:
4.1.
Calculul elementului din sirul Romberg: I1,K;
4.2.
Initializarea extrapolarii Richardson: j ¬ 2;
4.3.
Extrapolari Richardson iterative:
4.3.1.
Indice Richardson: k
¬
K-j+1;
4.3.2.
Elementul extrapolat:
![]()
4.3.3.
Abaterea la extrapolare: dI1¬ çIj,k
- Ij-1,k+1ú si dI2¬ Eps× çIj,kú
4.3.4.
Avans extrapolare: j¬j+1;
4.3.5.
Criteriul de oprire in bucla de extrapolare: daca j £ K si dI1 ³ dI2, se revine la pasul 4.3.1. In caz contrar,
se paraseste bucla de extrapolare si se trece la pasul 4.4.
4.4.
Incrementare contor: K¬K+1;
4.5.
Criteriul de oprire in bucla iterativa exterioara: daca
K £ Nmax si dI1
³ dI2, se revine la
pasul 4.1. In caz contrar, se intrerupe bucla iterativa si se trece la pasul 5.
5. Valoarea aproximativa a integralei se gaseste in Ij-1,k.