Metode numerice - Aplicatii
Lucrarea 12. Metode directe pentru rezolvarea ecuatiilor diferentiale ordinare: metoda Euler si metode de tip Runge-Kutta
Tema
A - Metoda Euler
Tema B - Metode Runge-Kutta
Exista
o serie de aplicatii practice care presupun studiul unor sisteme sau procese
dinamice. In acest caz se urmareste stabilirea legii de variatie a unei functii
y, care descrie starea sistemului. In general, functia y
depinde nu numai de una sau mai multe variabile independente x, ci si de alte valori ale sale
anterioare in raport cu una din variabilele independente, astfel spus de stari
anterioare ale sistemului. Asemenea probleme conduc la
modele matematice descrise de ecuatii diferentiale.
In cazul particular
al ecuatiilor diferentiale ordinare, orice problema descrisa de asemenea
ecuatii poate fi redusa la studiul unui sistem de ecuatii diferentiale de ordin
intai. De exemplu, ecuatia de ordinul doi :
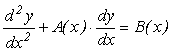
poate fi adusa la forma
a doua ecuatii diferentiale de ordinul intai:
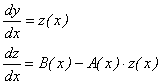
unde z(x) reprezinta o functie sau variabila
dependenta auxiliara. Cea mai la indemana solutie de alegere a functiilor
auxiliare z(x) consta in definirea
lor ca derivate ale functiei originare y(x)
sau ale functiilor auxiliare z(x)
precedente in succesiunea substitutiilor de tip (8.2). Prin urmare, problema
originara a ecuatiilor diferentiale ordinare poate fi redusa, in general, la
analiza unui sistem de n ecuatii
diferentiale de ordin intai scris pentru n
functii yi(x), i=1,...,n sub forma:
unde functiile fi descriu forme in general
neliniare in variabila independenta x
si cele n variabile dependente yi.
In general, acest
sistem de ecuatii diferentiale ordinare admite o infinitate de solutii. Pentru
particularizarea uneia dintre acestea, care sa
reprezinte solutia problemei studiate, este necesar ca ecuatiilor sa li se
asocieze o serie de conditii specifice problemei respective. Aceste
conditii impun de regula valori pentru functiile yi(x) in anumite puncte bine specificare. Pozitia
acestor puncte in domeniul variabilei x
pentru care se studiaza procesul determina tipul de problema si deseori chiar
si metoda de rezolvare ce trebuie folosita.
Se considera
problema numita cu conditii initiale
pentru care se indica valorile functiilor yi(x)
intr-un punct de referinta xR, considerat ca origine a procesului. Din considerente
legate de simplificarea notatiilor folosite si pentru o mai buna intelegere a
mecanismelor ce guverneaza diferitele metode numerice specifice, problema cu
conditii initiale va fi prezentata pentru cazul particular al ecuatiilor
diferentiale de ordin intai
(problema Cauchy) de
forma
si conditiei initiale:
Pentru forme
relativ simple ale ecuatiei prezentate,, problema Cauchy admite o rezolvare
analitica, care are avantajul de a determina in forma explicita legea de
variatie a functiei y cu variabila independenta x. Numeroase aplicatii practice conduc
la ecuatii diferentiale cu o forma complexa a expresiilor ce definesc
derivata dy/dx. Mai mult decat atat, uneori nici macar nu avem la dispozitie
asemenea expresii, ci doar valori ale lor in anumite puncte. Din aceste motive,
rezolvarea problemei se face pe cale numerica, cu
metode special dezvoltate in acest scop.
Ideea care sta la baza tuturor
metodelor numerice de rezolvare a ecuatiilor diferentiale ordinare cu conditii
initiale este urmatoarea: notatiile dy
si dx se inlocuiesc cu cresterile
finite Dy si Dx. Se obtine astfel o expresie algebrica care permite
calculul variatiei functiei y(x) la
modificarea variabilei independente x
cu un pas Dx. Aproximatia numerica obtinuta pe aceasta cale se va apropia
cu atat mai mult de solutia exacta cu cat pasul Dx va fi mai mic.
Metodele numerice de rezolvare a unei
ecuatii diferentiale
pornesc din punctul (x0,
y0) precizat de conditia initiala si, avansand cu pasul Dx, determina un sir de puncte (xk, yk), k=1, 2,... care descriu sub forma
numerica solutia problemei.
Conform principiului de baza, la fiecare iteratie
functia se aproximeaza prin adaugarea la valoarea curenta a unei corectii egala
cu produsul dintre pasul de integrare si derivata functiei. Din punct de vedere
formal, acest principiu descrie de fapt metoda
Euler:
Originea acestei
formule se gaseste insa in dezvoltarea in serii
Daca se cunoaste valoarea functiei in
punctul xk, notata yk=y(xk), functia f(x,y) ce defineste ecuatia diferentiala
ce defineste problema Cauchy permite calculul derivatelor de orice ordin y(q)(x) care apar in ultima relatie.
Astfel, pentru primele doua derivate, se poate scrie:
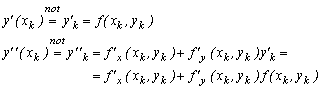
unde prin f’x si f’y s-au notat
derivatele partiale ale functiei f(x,y)
in raport cu x, respectiv y. Prin urmare, daca se
calculeazaderivatele y(q)(x)
, este posibila evaluarea functiei y(x)
in orice punct din vecinatatea lui xk.
Aceasta este o metoda numerica, cunoscuta sub numele
de metoda
sa se determine
solutia numerica a ecuatiei diferentiale sub forma unui sir de puncte (x0, y0), (x1,
y1), … , (xk, yk), … .Daca din
ultima relatie se retin numai primii doi termeni, se regaseste formula
corespunzatoare metodei Euler:
Marginea superioara
a erorii de trunchiere este:
unde x este un punct din
intervalul [xk, xk+1].
Algoritmul
1 – Metoda Euler
1.
Introducerea datelor initiale: functia f(x,y) din ecuatia diferentiala y’=f(x,y), pasul h de crestere a valorilor variabilei,
numarul de puncte de calcul al solutiei, N:
2.
Indicarea conditiilor initiale x0 si y0, unde y0=F(x0)
3.
Initializarea coordonatelor punctului de pornire x(1)= x0, y(1)= y0;
4.
Aplicarea formulei Euler:
for
k=1 to N-1 do
begin
y(k+1)=y(k)+f(x,
y(k))*h
x=x+h
end;
1.
Solutia aproximativa se gaseste in vectorul y[1..n].
In
cazul metodei Euler obisnuite deplasarea intre doua puncte de calcul succesive xk si xk+1, se face prin aplicarea unei corectii valorii yk determinata de produsul
pasului de integrare h si derivata
solutie y(x) calculata la
extremitatea stanga a intervalului yk,
folosind functia f ce defineste ecuatia diferentiala. Se poate scrie, asadar:
Pentru versiunea Cauchy, imbunatatirea
preciziei se obtine calculand corectia ce se aplica lui yk in functia de derivata lui y(x) la mijlocul intervalului de lucru xk+1/2=xk+h/2. Calculul derivatei in acest
punct necesita o aproximare pentru yk+1/2,
care se obtine folosind un pas Euler clasic, adica:
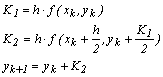
Metodele Runge–Kutta
generalizeaza acest principiu. Pornind de la un punct de coordonate cunoscute (xk,yk), metodele
Runge–Kutta avanseaza la punctul urmator aplicand valorii yk o combinatie liniara de
corectii Kj , ponderate de
o serie de coeficienti grj ce urmeaza a fi
determinati:
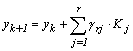
In
aceasta relatie r indica ordinul
metodei. Metodele de tip Runge–Kutta au o serie de avantaje dintre care
se amintesc: (i) sunt metode directe,
deci nu necesita folosirea unor metode auxiliare la pornire; (ii) sunt identice cu seriile Taylor
pana la termenul de rang r, deci exista
posibilitatea estimarii erorii de trunchiere; (iii) nu necesita evaluari ale derivatelor partiale ale functiei f(x,y), ci numai ale functiei f in sine.
Corectiile Kj se determina ca produs al pasului de integrare h cu anumite valori ale functiei f, calculate in puncte din vecinatatea
punctului (xk, yk):
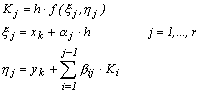
In toate cazurile
se considera:
deci: 
astfel incat se
poate scrie:
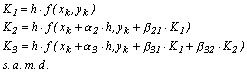
Mai ramane sa se
precizeze valorile coeficientilor grj, aj si bji. Acesti coeficienti se determina
impunand conditia ca formula 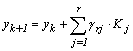Runge–Kutta sa coincida cu dezvoltarea in serii Taylor pana la rangul r. Se mentioneaza ca aceasta conditie
conduce la un sistem de ecuatii neliniare cu necunoscutele grj, aj si bji care, in general, contine mai putine ecuatii
decat necunoscute. Rezolvarea acestui sistem impune precizarea a priori a unora dintre necunoscute,
ceea ce face ca formula sa genereze un numar teoretic nelimitat de metode
Runge–Kutta. In practica, insa, o raspandire mai larga o cunosc numai
cateva asemenea metode. In continuare, se vor prezenta cateva cazuri
particulare de metode Runge–Kutta.
Cazul r=1 (Formula Runge–Kutta
de ordin intai) In
acest caz relatiile de calcul, impreuna cu restrictia g11=1, conduc la:
adica tocmai
formula metodei Euler obisnuite. Eroarea de trunchiere la un pas, este de
ordinul h2.
Cazul
r=2 (Formula Runge–Kutta de ordin doi)
Ecuatiile de calcul conduc in acest caz,
succesiv, la:
Pentru determinarea
coeficientilor necunoscuti aceasta expresie se dezvolta dupa puterile lui h in jurul punctului (xk, yk) si se retin
numai termenii liniari:
Pe de alta parte, dezvoltarea in serii
Impunand conditia
ca ultimele doua expresii sa coincida, rezulta:
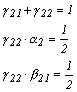
Daca
se impune a priori g21=0, rezulta: g22=1 si a2=b21=1/2, respectiv o prima
varianta de formula Runge–Kutta, de ordin doi:
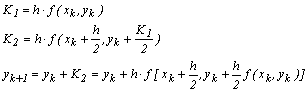
Daca
se impune g22=1/2, rezulta g21=1/2 si a2= b21=1, respectiv:
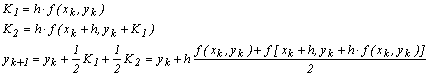
Aplicarea unui pas folosind
formulele genereaza o eroare de trunchiere de ordinul h3.
Cazul r=3 (Formula
Runge–Kutta de ordin trei) Folosind un
rationament similar celui desfasurat pentru r=2,
se ajunge la un sistem de sase ecuatii cu opt necunoscute. Formula
Runge–Kutta de ordin trei cea mai
uzuala este:
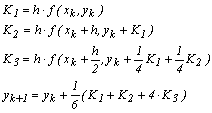
Fiind vorba de o
metoda de ordin trei, eroarea de trunchiere asociata este de ordin h4.
Cazul r=4 (Formula Runge–Kutta
de ordin patru) Aceasta
este metoda Runge–Kutta cel mai
frecvent utilizata in practica si foloseste un sistem de coeficienti care
conduce la formula:
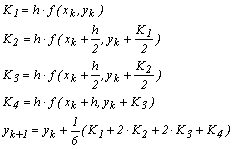
Metoda
Runge–Kutta de ordin patru are o
eroare de trunchiere de ordin h5.
Algoritmul 2 – Metoda Runge-Kutta de
ordin 4
1.
Introducerea datelor initiale: functia f(x,y) din ecuatia diferentiala y’=f(x,y), pasul h de crestere a valorilor variabilei,
numarul de puncte de calcul al solutiei, N:
2.
Indicarea conditiilor initiale x0 si y0, unde y0=f(x0)
3.
Initializarea coordonatelor punctului de pornire x(1)= x0, y(1)= y0;
4.
Aplicarea formulei Runge-Kutta:
for
i=1 to N-1 do
begin
4.1.
Calculul coeficientilor K1-K4 in punctual current, de coordinate (x(i), y(i)):
K1=f(x(i), y(i))*h
K2=f(x(i)+h/2,
y(i)K1/2)*h
K3=f(x(i)+h/2,
y(i)K2/2)*h
K4=f(x(i)+h, y(i)+K3)*h
4.2
Calculul valorii functiei y in punctul de abscisa x(i+1)
end;
5.
Solutia aproximativa se gaseste in vectorii x[1..n] si y[1..n].
Aplicatii - Lista lucrarilor de laborator