Metode
numerice - Aplicatii
Lucrarea
14.
Metode partiale pentru calculul valorilor si vectorilor proprii: metoda puterii
directe, metoda puterii inverse, metoda puterii inverse cu decalaj spectral,
metoda iterativa inversa cu coeficient Rayleigh
Tema A: Metoda puterii directe
Tema
B: Metoda puterii inverse
Tema
C: Metoda puterii inverse cu decalaj spectral
Tema
D: Metoda iterativa inversa cu coeficient Rayleigh
Daca
unui vector n – dimensional x i se aplica o transformare definita
de matricea A de dimensiune n × n,
se obtine vectorul y=A×x. Nu întotdeauna
între vectorii x si y astfel definiti exista o corelatie
bine precizata, adica ei pot avea orientari oarecare. Exista însa anumiti vectori x pe care
matricea A îi transforma în multipli
ai lor însisi. Pentru o matrice reala, patrata A, de dimensiuni n× n, exista, în general, cel putin n vectori x pe care
transformarea liniara A îi lasa
invarianti ca directie, adica îi transforma în vectori proportionali cu ei
însisi:
![]()
Factorul
de proportionalitate l se numeste valoare proprie a matricei A, iar vectorul x – vector propriu
asociat valorii proprii l.
Pentru determinarea valorilor proprii ale
matricei A, relatia de definitie
poate fi scrisa în forma echivalenta:
![]()
unde In este matricea unitate de
rang n. S-a obtinut astfel un sistem
omogen de ecuatii liniare care admite o solutie diferita de solutia banala
– deci vectori proprii nenuli – daca determinantul sau se anuleaza:
![]()
care reprezinta ecuatia caracteristica a matricei A. Scalarii l care verifica
ultima relatie sunt tocmai valorile proprii ale acestei matrice. Prin
dezvoltarea determinantului dupa regulile cunoscute se obtine un polinom de
grad n în l, cu coeficienti
reali, numit polinom caracteristic:
![]()
ale carui radacini sunt valorile proprii.
Metodele numerice directe determina valorile proprii
prin rezolvarea ecuatiei caracteristice. Se prezinta in
continuare metoda puterii directe, metoda puterii inverse si varianta
acesteia cu deplasarea originii.
Acestea se mai numesc metode
partiale, deoarece determina numai anumite valori si vectori proprii ale
unei matrice.
Tema A: Metoda puterii directe
Vom
considera problema initiala A×x=l× x pentru care se
admite ca matricea A este
nedefectiva, adica are exact n
vectori proprii liniar independenti, care formeaza o baza în spatiul real n-dimensional. De asemenea, se admite ca
sistemul celor n vectori proprii x1, x2,…,
xn este un sistem
normalizat dupa norma infinita, deci componenta maxima a fiecarui vector este
egala cu unitatea. Metoda puterii directe, denumita uneori prescurtat metoda puterii, determina valoarea proprie maxima în
modul a matricei A si vectorul
propriu asociat acesteia.. În acest context, vom adopta ipoteza suplimentara conform careia
matricea A are o valoare proprie
dominanta si aceasta este prima :
În aceste conditii, orice vector y din spatiul n-dimensional se poate exprima ca o combinatie liniara a vectorilor
proprii:
Dupa cum spune si numele ei, metoda
puterii directe apeleaza la construirea unui sir de vectori normalizati, pe baza unei relatii de
recurenta dupa puterile matricei A. Astfel, pornind de la y(0) = y (cu ![]() =1),
se construieste sirul de vectori y(0),
y(1),…, y(k) :
=1),
se construieste sirul de vectori y(0),
y(1),…, y(k) :
![]() k=0,1, ...
k=0,1, ...
unde y(k+1)
se obtine prin normalizarea lui y’(k+1), iar ![]() . Daca se dau succesiv lui k valorile 0, 1, 2,
…., se obtine:
. Daca se dau succesiv lui k valorile 0, 1, 2,
…., se obtine:
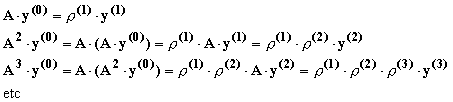
sau relatia de
recurenta:
![]() ,k=1,2,
...
,k=1,2,
...
Deoarece r(1), r(2), ...
, r(k) sunt marimi
scalare de normalizare, rezulta ca vectorul Ak×y(0) este coliniar cu y(k).
Pe de alta parte, avand în vedere descompunerea vectorului y(0) dupa baza x1,
x2,…., xn
si proprietatea A×xi=li × xi, se poate scrie:
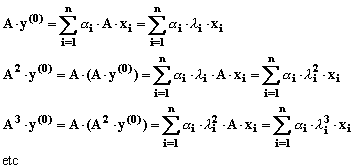
sau, în general:
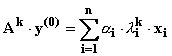 k=1,2, ...
k=1,2, ...
Daca
se tine seama de caracterul dominant al valorii proprii l1 si se izoleaza
termenul de rang i=1 din ultima
relatie:
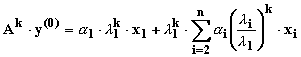 ,k=1,2, ...
,k=1,2, ...
se verifica imediat
ca, pentru k ® ¥, termenii sumei
din se pot considera oricat de mici, iar
prin neglijarea lor rezulta:
![]() ,k=1,2, ...
,k=1,2, ...
Se poate afirma ca
la limita vectorul y(k)
tinde spre vectorul propriu x1.
Un rationament simplu arata ca la
limita (k ®
¥) parametrul de
normalizare r(k+1) tinde chiar catre
valoarea proprie l1 cautata.
Într-adevar, pentru k suficient de
mare, diferenta y(k+1)-y(k) tinde
spre 0 si se poate scrie:
![]()
Daca în aceasta
relatie se tine seama si de expresia ![]() , se
obtine:
, se
obtine:
![]()
adica, la limita r(k+1) este valoarea proprie
asociata vectorului propriu y(k). Deoarece însa, asa cum am aratat mai sus,
vectorul y(k)
tinde catre vectorul propriu x1, înseamna ca parametrul
de normalizare r(k+1) va aproxima valoarea proprie dominanta l1.
Convergenta metodei
puterii directe, depinde esential de viteza cu care rapoartele (li/l1)k tind catre 0. În practica,
metoda puterii directe se dovedeste eficienta mai ales în cazul matricelor A caracterizate
de o valoare proprie net superioara în valoare absoluta celorlalte.
Algoritmul 1 – Metoda puterii directe
1.
Definirea
matricei A=[aij], i,j=1,...,n si a preciziei Eps.
2.
Aproximatia initiala a vectorului propriu y1 ¬ [1 0 ... 0]T
si initializarea parametrului de normalizare r(1)¬ 1.
3.
Proces iterativ pentru determinarea perechii vector
propriu-valoare proprie dominanta (x1,l1):
3.1.
Initializarea contorului de iteratii: k¬ 0;
3.2.
Trecerea la o noua iteratie: k ¬ k+1;
3.3.
Calculul noii aproximatii: y'(k+1) ¬ A×y(k)
3.4.
Calculul parametrului de normalizare: r(k+1)¬ ![]()
3.5.
Normalizarea noii aproximatii: ![]()
3.6.
Conditia de oprire: daca ![]() £ Eps
procesul iterativ se întrerupe si se trece la pasul
4. În caz contrar se revine la pasul 3.2.
£ Eps
procesul iterativ se întrerupe si se trece la pasul
4. În caz contrar se revine la pasul 3.2.
4.
Valoarea proprie dominanta a matricei A este l1 ¬ r(k+1), iar vectorul propriu
asociat este x1 ¬ y(k+1).
Tema B: Metoda puterii inverse
Una dintre
proprietatile valorilor si vectorilor proprii afirma ca daca l este o valoare
proprie a matricei A nesingulare, atunci 1/l este valoarea
proprie a inversei A-1, iar cele doua matrice au acelasi sistem de vectori proprii. În contextul acestei
proprietati, daca l este valoarea
proprie a lui A, minima în modul, 1/l va reprezenta valoarea
proprie dominanta a inversei A-1.
Prin urmare, daca se aplica metoda puterii directe matricei A-1, se determina de fapt valoarea proprie minima în
modul a matricei A. Acest procedeu
poarta numele de metoda puterii inverse.
Se admite ca vectorii proprii ai
matricelor A si A-1 sunt liniar independenti si formeaza o baza în spatiul real n-dimensional. Orice vector y poate fi exprimat ca o combinatie
liniara a vectorilor proprii:
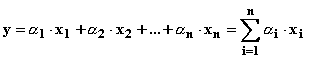
De aceasta data, se
face ipoteza conform careia valoarea proprie minima în modul a matricei A este ultima:
![]()
Metoda
puterii inverse construieste un sir de vectori y(0), y(1),...,y(k) pe baza relatiei de
recurenta:
![]() k=0,1, ...
k=0,1, ...
Printr-un
rationament analog celui prezentat în paragraful anterior, se poate arata ca
pentru valori suficient de mari ale lui k (k ® ¥), vectorul y(k) tinde catre
vectorul propriu xn, iar parametrul de normalizare r(k+1) tinde catre
inversa valorii proprii ln.
Algoritmul asociat acestei metode este
prezentat în continuare.. Mai întai
, inversarea matricei a se face printr-o procedura de factorizare, iar in continuare, cu inversa A-1 se calculeaza valoarea proprie si vectorul propriu
dorite.
Algoritmul
2 – Metoda puterii inverse
1.
Definirea matricei A =[ a
ij ], i,j=1,...,n
si a preciziei Eps
2. Aproximatia initiala a vectorului propriu y1 ¬ [1 0 ... 0]T si initializarea parametrului de normalizare r(1)¬ 1.
3. Inversarea matricei A: A-1.
4. Proces iterativ pentru determinarea perechii vector propriu-valoare proprie dominanta a inversei A-1:
4.1.
Initializarea contorului de iteratii: k¬ 0;
4.2.
Trecerea la o noua iteratie: k ¬ k+1;
4.3.
Calculul noii aproximatii: y'(k+1) ¬ A-1×y(k)
4.4.
Calculul parametrului de normalizare: r(k+1)¬ ![]()
4.5.
Normalizarea noii aproximatii: ![]()
4.6.
Conditia de oprire: daca ![]() £ Eps procesul iterativ
se întrerupe si se trece la pasul 5. În caz contrar se revine la pasul 4.2.
£ Eps procesul iterativ
se întrerupe si se trece la pasul 5. În caz contrar se revine la pasul 4.2.
5.
Valoarea proprie minima în modul a matricei A este ln ¬ 1/r(k+1), iar vectorul
propriu asociat este xn ¬ y(k+1).
Tema C: Metoda puterii inverse cu decalaj spectral
Un
procedeu mult mai eficient de calcul al tuturor valorilor proprii ale unei matrice
folosind metoda puterii inverse implementeaza Algoritmul 2 nu matricei A, ci unei matrice decalate
A-q×In unde q
este un scalar ce realizeaza translarea originii. Metoda care rezulta poarta
numele de metoda puterii inverse cu
deplasarea originii sau metoda
iterativa inversa cu decalaj spectral. Algoritmul de aplicare este
asemanator cu cel al metodei puterii inverse, însa de aceasta data parametrul
de normalizare r(k+1) tinde catre
marimea 1/(lq-q), unde
lq este valoarea
proprie a matricei A cea mai
apropiata de scalarul q.
Prin urmare, localizarea cu suficienta
precizie a valorilor proprii si aplicarea metodei puterii inverse cu decalaj
spectral permit calculul tuturor valorilor proprii, fara a
impune nici o restrictie asupra ordinii în care se calculeaza acestea. De altfel, majoritatea lucrarilor de
specialitate recomanda aceasta metoda ca pe una dintre cele mai puternice
tehnici de calcul a valorilor si vectorilor proprii, în special în cazul unor
matrice de dimensiuni nu prea mari.
Singurul dezavantaj al metodei
iterative inverse cu decalaj spectral consta în necesitatea redefinirii
matricei decalate A-q×In si recalcularii
inversei sale pentru fiecare valoare proprie ce se
determina. O alta particularitate a acestei metode este asa-numitul paradox al iteratiei inverse cu decalaj spectral,
conform caruia convergenta metodei este cu atat mai lenta cu cat decalajul
spectral q este mai aproape de
valoarea proprie cautata l. Într-adevar, pornind de la formula problemei
decalate:
(A - q×In) × x = (l - q) × x
se observa ca, la
limita, cand q ® l, relatia conduce la un sistem omogen de ecuatii
liniare, pentru care existenta unei solutii diferita de solutia banala impune
singularitatea matricei A-q×In. Prin urmare,
neexistand inversa (A-q×In)-1,
nici metoda puterii inverse nu poate fi aplicata.
Tema D: Metoda
iterativa inversa cu coeficient Rayleigh
Aplicarea cu succes a metodei
iterative cu decalaj spectral presupune o initializare cat mai rationala a
decalajului q, adica a aproximatiei initiale pentru valoarea proprie cautata. O
asemenea initializare poate folosi catul
Rayleigh definit pentru un vector x în raport cu o matrice A:
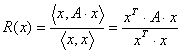
unde parantezele
unghiulare denota produsul scalar a doi vectori. De ce o asemenea initializare ? Pentru a raspunde la aceasta întrebare, se
considera formularea initiala a problemei
(A×x=l×x), care se înmulteste la stanga cu xT si se extrage apoi expresia valorii proprii:
![]()
Comparand relatiile se
observa imediat ca, atunci cand x este un vector propriu al matricei A, catul Rayleigh asociat coincide cu
valoarea proprie corespunzatoare. Prin urmare, utilizarea
expresiilor anterioare înlocuieste stabilirea aproximatiei initiale a valorii
proprii l cu cea a vectorului
propriu x asociat acesteia.
În loc sa se "ghiceasca" o singura valoare, adica l, se determina n
valori, adica cele n componente ale
vectorului propriu x, pe baza stationaritatii catului Rayleigh în vecinatatea vectorului propriu cautat.
Aceasta proprietate se traduce prin variatii "relativ slabe" ale
catului Rayleigh la variatii "relativ însemnate" ale vectorului x.
Prin urmare, pornind de la o aproximatie "grosiera" a
vectorului propriu x, catul Rayleigh
reprezinta , în general, o aproximatie
"excelenta" pentru valoarea proprie asociata. Acesta este de fapt raspunsul la paradoxul iteratiei inverse cu
decalaj spectral.
Algoritmul
3 – Metoda iterativa
inversa cu coeficient Rayleigh
1.
Definirea matricei A=[aij],
i,j=1,...,n si a preciziei Eps.
2.
Aproximatia initiala a vectorului propriu x1 si normalizarea acesteia.
3.
Calculul catului Rayleigh asociat aproximatiei
initiale:
R1 ¬ ![]()
4.
Initializarea procesului iterativ: k ¬ 0.
5.
Aplicarea metodei iterative inverse cu decalaj
spectral:
5.1.
Trecerea la o noua iteratie: k ¬ k+1;
5.2.
Aplicarea decalajului spectral matricei A folosind catul Rayleigh:
As ¬ A - Rk × In.
5.3.
Calculul inversei matricei decalate As-1.
5.4.
Calculul noii aproximatii a vectorului propriu:
xk+1 ¬ As-1 × xk
5.5.
Normalizarea noii aproximatii:
![]()
5.6.
Calculul catului Rayleigh pentru noua aproximatie:
Rk+1 ¬ ![]()
5.7.
Criteriul de oprire: daca çRk+1
- Rkú £ Eps sau k=Nmax procesul iterativ se întrerupe si
se trece la pasul 6. În caz contrar se revine la pasul 5.1.
6. Perechea valoare proprie-vector propriu cautata este (l,x) º ( Rk+1,xk+1).
Se
poate arata ca, daca aproximatia initiala x1
nu este ortogonala pe vectorul propriu cautat x, utilizarea catului Rayleigh ca aproximatie a valorii proprii l asigura o
convergenta patratica, adica úçxk+1
- xúç £ d ×úçxk+1
- xúç2 , unde d este un scalar
strict pozitiv. Mai mult chiar, daca matricea A este simetrica, procesul iterativ se caracterizeaza
printr-o convergenta cubica. Aceste proprietati excelente de convergenta sunt
însa compensate în buna masura de efortul marit de calcul determinat de
necesitatea recalcularii la fiecare iteratie a
inversei matricei decalate As. Aceasta reprezinta
o piedica serioasa în calea utilizarii pe scara larga a metodei iterative
inverse cu decalaj spectral.