1. Perceptronul
multistrat
Într-o
reţea de tip PMS neuronii ascunşi pot fi priviţi ca noduri ale
reţelei în care informaţia de intrare este „reprezentată”
într-un format intern, astfel încât
să se asigure
simplificare la maximum
a sarcinilor de prelucrare care revin neuronilor din
stratul de ieşire. Din acest motiv, se spune că stratul ascuns
asigură formarea unei reprezentări interne a informaţiei de
intrare / ieşire, care nu este conţinută explicit în setul de
antrenare.
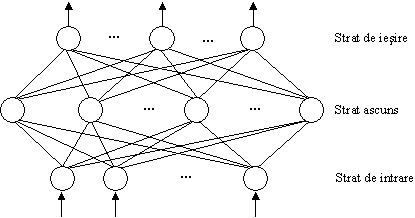
În cazul
unei reţele de tip PMS care modelează o problemă oarecare, cea
mai dificilă sarcină o reprezintă stabilirea unui procedeu care
să permită formarea unei reprezentări interne cât mai potrivite
în stratul ascuns. Este evident că, pentru problemele complexe,
identificarea riguroasă a reprezentărilor pe care le asigură
fiecare neuron din stratul ascuns nu mai este posibilă. Procedura care
permite formarea unor asemenea reprezentări interne, chiar dacă
acestea se dovedesc de cele mai multe ori total netransparente, constă în
ceea ce este cunoscut sub numele de învăţare sau antrenare
a reţelei neuronale.
Forma generalizată a regulii D
Algoritmul
de retropropagare a erorii propus de este denumit uneori şi forma
generalizată a regulii D. Acest algoritm, porneşte de la un set de
date de antrenare format din perechi intrare – ieşire dorită
foarte asemănător modului de definire tabelară a funcţiilor
în vederea aproximării. Ponderile reţelei neuronale de tip PMS se
iniţializează cu valori aleatorii, alese de obicei în intervalul (-1,
1).
Aplicarea
algoritmului de retropropagare se face în următoarele ipoteze: (i)
se consideră cazul unei reţele de tip PMS care foloseşte neuroni
ascunşi; (ii) funcţiile de
activare ale neuronilor
ascunşi şi ale celor de ieşire se consideră continue şi derivabile;
(iii) dacă este cazul, mărimile de ieşire se
scalează în intervale corespunzătoare funcţiei de activare
folosite. Funcţionarea algoritmului de retropropagare se
desfăşoară în două etape:
(a) se
consideră un model m din setul de date de antrenare (o linie din
tabelul de definiţie), din care se extrag mărimile de intrare –
vectorul x(m) – care se aplică pe intrarea
reţelei şi, folosind valorile curente ale ponderilor, se face
propagarea înainte a informaţiei de intrare, calculându-se ieşirea
reală furnizată de reţea, o(m).
(b)
ieşirea reală o(m) se
compară cu valoarea dorită d (m)
corespunzătoare setului de antrenare şi eroarea astfel calculată
se propagă înapoi în reţea – de la stratul de ieşire, spre
stratul de intrare – pentru modificarea ponderilor.
Regula sau algoritmul de antrenare folosit stabileşte
tocmai metoda de ajustare a ponderilor din reţea. În cazul formei
generalizate a regulii D,
ajustarea ponderilor se face în sensul minimizării abaterii între valorile
reală o(m) şi dorită d(m) de pe
ieşirea reţelei. Dacă paşi (a) şi (b) de mai sus se
reiau pentru următorul model din setul de antrenare (m ¬ m
+ 1), ponderilor li se va aplica o nouă corecţie în raport cu
ieşirile o(m + 1) şi d (m
+ 1). După epuizarea tuturor modelelor din setul de antrenare, se
spune că s-a efectuat un ciclu de antrenare. Este de aşteptat
ca, pe măsura considerării de noi modele din setul de antrenare,
abaterile o(m) – d (m)
să se micşoreze, în general, pentru toate modelele. De cele mai multe
ori, însă, un singur ciclu de antrenare nu este suficient pentru aproximarea
cu suficientă precizie a tuturor valorilor de ieşire indicate în
setul de antrenare. Ca urmare, algoritmul se reia pentru un nou ciclu şi
procesul continuă, până la satisfacerea unui anumit criteriu de
oprire.
Forma
generalizată a regulii D propusă
de Rumelhart este descrisă de următoarele trei propoziţii:
(1)
Pentru fiecare model de intrare – ieşire m din
setul de antrenare, corecţia unei ponderi wij –
notată D(m)wij – pentru
conexiunea dintre neuronul j şi neuronul i din stratul
inferior este proporţională cu un termen de eroare dj(m) asociat
neuronului j:
unde oi(m)
este ieşirea neuronului i din stratul inferior, pentru modelul m,
iar h este un
factor de proporţionalitate, numit rată de învăţare.
(2) Dacă
neuronul j se află în stratul de ieşire, termenul de eroare dj(m) se
calculează în funcţie de abaterea între valoarea reală oj(m)
şi cea dorită dj(m) şi derivata
funcţiei de activare f a neuronului j în raport cu intrarea
netă corespunzătoare modelului m, notată netj(m):
(3)
Dacă neuronul j se află în stratul ascuns
(Fig. 4.4.b), fiind legat prin conexiuni sinaptice cu neuronii k din
stratul de ieşire, termenul de
eroare dj(m) este
proporţional cu suma tuturor termenilor de eroare asociaţi neuronilor
de ieşire k, modificaţi de ponderile conexiunilor respective wjk
şi cu derivata funcţiei de activare în raport cu intrarea netă netj(m):
Propoziţiile
(2) şi (3) arată că ponderile asociate unui anumit neuron sunt
ajustate cu termeni direct proporţionali cu abaterile dintre mărimile
reale şi cele dorite corespunzătoare neuronilor cu care
primul este legat.
Algoritmul de retropropagare – forma elementară
Cea mai simplă formă de
implementare a algoritmului de retropropagare foloseşte organigrama din
Fig. 4.9.a, fără a aplica nici o tehnică specială pentru
adaptarea parametrilor de antrenare. Acest algoritm este prezentat în Caseta
4.1.
Utilizarea algoritmului descris în
Caseta 4.1 presupune specificarea unor valori pentru ratele de
învăţare h1 şi h2. În
general, se pot folosi valori distincte pentru fiecare din ponderile v
şi w sau o valoare unică, comună. Ca regulă
generală, pentru ratele de învăţare h1 şi h2 se recomandă
valori între 0.2 şi 0.4.
Forma
elementară a algoritmului de retropropagare.
1. Definirea arhitecturii reţelei
PMS: numărul de neuroni de pe fiecare strat (I, J, K)
şi setul de date de antrenare: {x(m), d(m)}
m = 1,…,M. Definirea numărului de cicluri de antrenare: Cmax.
2. Definirea parametrilor reţelei:
ratele de învăţare pentru ponderile v şi w, notate
h1, respectiv h2.
3. Iniţializarea ponderilor
reţelei cu valori aleatorii în intervalul (-1, 1):
vjk
= 2 × random( ) – 1;
wij = 2 × random( ) – 1 (i = 1,…,I; j = 1,…, J; k = 1,…,K).
4. Ajustarea poderilor:
for c
= 1 to Cmax do.
for m = 1 to M do.
// Propagare înainte în primul
strat
for j = 1 to J do
yj = 0;
for i = 1 to I do yj
= yj + wji × xi
// Propagarea înainte în al doilea
strat
for k = 1 to K do
ok = 0;
for j = 1 to J do ok
= ok + vkj × yj
for j = 1 to J do
// Adaptarea ponderilor
pentru al doilea strat
for k = 1 to K do
// Adaptarea ponderilor pentru
primul strat}
for i = 1 to I do
5. Reţeaua
a fost antrenată pe cele M modele, în Cmazx
cicluri, iar caracteristicile sale se găsesc în ponderile vjk
şi wij.
2. Reţele
neuronale artificiale pentru clasificare şi recunoaştere
Într-un
context general, clasificarea poate fi definită ca acel proces de
învăţare a asemănărilor şi deosebirilor dintre modele,
care reprezintă instanţe ale unor obiecte dintr-o populaţie de
obiecte neidentice. În cadrul unui proces de clasificare, obiectele sânt
grupate în clase, conform asemănărilor şi deosebirilor
sesizate. Astfel, pornind de la atribute specifice fiecărui obiect, se
formează clase care descriu proprietăţile generale ale
obiectelor respective. Obiectivul final al oricărui proces de clasificare
este acela de a permite sistemului să identifice / recunoască
obiectele din mediul său, pe baza proprietăţilor ce
caracterizează clase de obiecte.
În
consecinţă, în contextul problemei de clasificare, un sistem trebuie
să parcurgă două etape: (a) clasificarea, în cursul
căreia sistemul învaţă caracteristicile generale ale claselor pe
baza caracteristicilor specifice instanţelor şi (b) recunoaşterea,
în cursul căreia sistemul suprapune caracteristicile unei instanţe
peste caracteristicile claselor cunoscute şi identifică clasa
căreia aparţine instanţa respectivă.
Pentru
majoritatea reţelelor neuronale artificiale prezentate în capitolele
anterioare s-a considerat că, pentru fiecare model din setul de antrenare,
se cunosc atât vectorul de intrare, cât şi vectorul de ieşire. Toate
algoritmele de antrenare prezentate încearcă să modifice structura
reţelei (valorile ponderilor conexiunilor şi pragurilor neuronilor)
astfel încât să asigure o corespondenţă cât mai bună între
intrările şi ieşirile reţelei neuronale. Acest model de
antrenare este cunoscut sub numele de învăţare supravegheată.
În sinteză, se poate spune că orice model de antrenare pentru care se
cunosc mărimile de ieşire intră sub incidenţa
învăţării supravegheate.
Există
însă numeroase situaţii practice – mai cu seamă în problemele de
clasificare – în care nu se cunoaşte în prealabil răspunsul pe care
ar trebui să-l furnizeze reţeaua pentru un anumit vector de intrare.
În asemenea cazuri ar fi de dorit ca reţeaua să identifice de una
singură caracteristicile datelor de intrare. Altfel spus, reţeaua ar
trebui să “înţeleagă“ singură modul în care trebuie
să organizeze informaţia. Asemenea procese sunt cunoscute sub numele
de auto-organizare sau învăţare nesupravegheată
şi tratează cu precădere probleme de clasificare.
În cazul
proceselor de auto-organizare, clasificarea mai este denumită şi zonare
(în engleză, clustering). Această denumire provine de la
dispunerea punctelor corespunzătoare vectorilor de intrare în anumite
zone, sub forma unor nori sau ciorchini. În interiorul unei asemenea zone
punctele sunt mai apropiate între ele sau în raport cu un centru comun, decât
în raport cu centrele altor zone.
Formele de principiu
ale algoritmelor de clasificare supravegheată şi auto-organizare sunt
indicate mai jos.
Algoritm supravegheat de clasificare
1. 1. Date de
intrare: modelele de antrenare, în perechi intrare–ieşire, {x(m)
, d(m)} m = 1,…,M.
2. 2. Dispunerea modelelor de intrare–ieşire
în ordine aleatorie {x(m) , d(m)}
m = 1,…,M.
3. Pentru fiecare model de antrenare m = 1,…,M se
ajustează parametrii reţelei astfel încât vectorului de intrare x(m)
să i se asocieze la ieşire vectorul dorit d(m).
Algoritm de clasificare prin auto – organizare.
1. Date de
intrare: modelele de antrenare, sub forma vectorilor de intrare x(m),
m = 1,…,M.
2. Dispunerea
modelelor de antrenare în ordine aleatorie {x(m)} m = 1,…,M.
3. Formarea
primei clase (K ¬ 1) prin
asocierea la aceasta a primului vector din setul de antrenare x(1),
ca prototip.
4. Tratarea
modelelor de antrenare.
4.1. Iniţializarea
numărului de ordine al modelelor: m = 2.
4.2. Selectarea
vectorului de intrare x(m).
4.3. Compararea
modelului x(m) cu prototipurile claselor existente:
4.3.1. Iniţializarea
numărului de ordine al clasei: k = 1.
4.3.2. Dacă
modelul x(m) este similar cu prototipul clasei Ck,
se trece la pasul 4.3.3. În caz contrar, se trece la pasul 4.3.4.
4.3.3. Asocierea
vectorului x(m) clasei Ck şi
trecerea la pasul 4.5.
4.3.4. Trecerea
la o nouă clasă: k ¬ k + 1. Dacă k Ł K
, se revine la pasul 4.3.2. În caz contrar, se trece la pasul 4.4.
4.4. Se creează
o nouă clasă (K ¬ K + 1), se asociază vectorul x(m)
clasei CK şi se iniţializează prototipul
acestei clase cu modelul x(m).
4.5. Trecerea
la un nou model de antrenare: m ¬ m + 1. Dacă m Ł M,
se revine la pasul 4.2. În caz contrar, se trece la pasul 5.
5.
Reţeaua a identificat K clase, fiecare dintre
acestea având asociat un anumit prototip.
Algoritmul celor mai apropiaţi k
vecini
Probabil
că acesta este cel mai simplu şi direct algoritm de clasificare.
Principiul acestui algoritm constă în selectarea dintre vectorii deja clasificaţi
a primilor k (valoarea lui k este precizată a priori), cei
mai apropiaţi de vectorul curent şi clasificarea acestuia din
urmă în clasa dominantă asociată celor k vectori de
referinţă.
Astfel,
se porneşte de la setul de învăţare format din vectorii {x(1),
x(2), … , x(M)} şi
de la numărul de clase C în care se face clasificarea. Atunci când
unul din aceşti vectori x(m) este asociat unei
clase c, se foloseşte notaţia: Clasa(m) = c.
După reordonarea aleatorie a vectorilor x(m) din
setul de antrenare se consideră arbitrar că primii C vectori
sunt incluşi fiecare în una din cele C clase. În continuare, pentru
fiecare din restul vectorilor x(C+1),
x(C+2), … , x(M) se parcurg următorii paşi:
(a) se
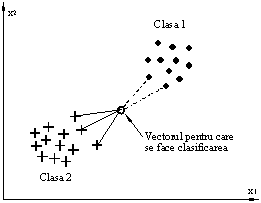
calculează
distanţele faţă de vectorii deja clasificaţi; (b) se
ordonează crescător aceste distanţe şi se consideră
vectorii corespunzători primelor k distanţe reordonate; (c)
pentru aceşti k vectori se determină clasa dominantă iar
vectorul curent se asociază acestei clase.
Descrierea mai detaliată a algoritmului
celor mai apropiaţi k vecini este prezentată mai jos. Deşi
este foarte simplu, acest algoritm prezintă totuşi unele
inconveniente. În primul rând, necesită precizarea a priori a
numărului de clase ce urmează a fi separate. Pe de altă parte,
chiar principiul celor mai apropiaţi vecini compară vectorul curent
cu vectori care, în majoritatea cazurilor, se găsesc către periferia
zonelor asociate fiecărei clase. Astfel asocierea la o clasă anume
ignoră vectorii care se găsesc în centrul acelei zone şi care
caracterizează de fapt cel mai bine clasa respectivă. Ca urmare, este
posibil ca asocierea la o anumită clasă să fie forţată
de unul sau doi vectori periferici, care caracterizează prea puţin
clasa respectivă (vezi figura de ,mai sus).
Algoritmul celor mai
apropiaţi k vecini.
1. Date de
intrare: modelele de antrenare, sub forma vectorilor de intrare x(m)
, m = 1,…, M; parametrul k (numărul de vecini);
numărul de clase C.
2. Reordonarea
aleatorie a vectorilor de antrenare {x(m)} m = 1,…,M.
3. Asocierea
primelor C modele la cele C clase:
for c = 1 to C do Clasa(c)
= c
4. Asocierea claselor pentru restul modelelor de antrenare:
for m = C +1 to M
do
// Calculează distanţele
faţă de vectorii deja clasificaţi
for q = 1 to m - 1 do
d(q) =
||x(m) – x(q)||
// Ordonează crescător
distanţele d(q) prin reordonarea indecşilor q
for i = 1 to m –
1 do
Ix(i) = i
for i = 1 to m – 2 do
for j = i + 1 to m – 1
do
if d(Ix( j))
< d(Ix(i))
then Ix( j) ¨ Ix(i)
// Calculează numărul de vectori asociaţi fiecărei
clase pentru primele k
// distanţe d(q), corespunzător indecşilor
reordonaţi
vmax = 0;
for c = 1 to C do
v = 0
for j = 1 to k do
if Clasa(Ix( j)) = c then
v = v + 1
if v > vmax then
Clasa(m) = c
vmax = v
Algoritmul
C- medii
Algoritmul
c-medii [MacQueen 67] introduce pentru prima dată
noţiunea de prototip sau vector-centru sau vector de
codare, care descrie în mod unitar o clasă. Astfel, pentru o
clasă c, prototipul z(c) se
calculează ca medie aritmetică a celor n(c) vectori ce
au fost asociaţi clasei respective:
z(c)
= 
x(m) "
m, cu proprietatea 
Şi
în acest caz se porneşte de la setul de antrenare {x(1),
x(2), … , x(M)} şi
de la numărul de clase C < M care trebuie
separate. După reordonarea
aleatorie a setului de antrenare, se atribuie arbitrar primele C
modele de antrenare celor C clase, vectorii x(1), … , x(C)
devenind prototipurile z(1), … , z(C).
În continuare, fiecare din restul de M – C modele de antrenare
este asociat unei clase, pe baza distanţelor minime faţă de cel
C prototipuri. Urmează recalcularea prototipurilor claselor şi noile
asocieri. Procesul se reia, până când – în două iteraţii
succesive – prototipurile claselor nu se schimbă sau se schimbă
într-o măsură considerată nesemnificativă.
O măsură care permite evaluarea
dimensiunilor zonei din spaţiul de definiţie acoperită de
fiecare clasă este abaterea medie pătratică dintre prototipul
clasei şi vectorii din setul de antrenare asociaţi acesteia,
notată 
:
||x(m) – z(c)||2 " m, cu
proprietatea 
Abaterea
pătratică totală:
reprezintă o
măsură a preciziei de clasificare la nivelul întregului set de
antrenare şi poate fi folosită pentru optimizarea numărului de
clase C (algoritmul este aplicat pentru valori diferite ale
numărului de clase C şi se alege varianta cu abaterea
pătratică totală 
minimă).
Algoritmul c–medii.
1. Date de
intrare: modelele de antrenare, sub forma vectorilor de intrare x(m)
, m = 1,…, M; numărul de clase C.
2. Reordonarea
aleatorie a vectorilor de antrenare {x(m)} m = 1,…,M.
3. Asocierea
primelor C modele la cele C clase:
for c = 1 to C do
z(c) = x(c)
; n(c) = 0
4. Asocierea fiecărui model de antrenare
la clasa cu prototipul cel mai apropiat:
for m = 1 to M do
Dmin = 106
// Iniţializarea
distanţei minime
for
c = 1 to C do
if ||x(m) – z(c)||
< Dmin then
Dmin = ||x(m)
– z(c)||
Cmin = c
Clasa(m)
= Cmin
n(Cmin) = n(Cmin)
+ 1
5. Calculul
noilor prototipuri pentru cele C clase:
for c = 1 to C do
w(c)
= 0
for m =1 to
M do
if Clasa(m)
= c then
w(c) = w(c)
+ x(m)
w(c)
= w(c) / n(c) // Prototipuri temporare
6.
Calculul abaterilor pătratice:
sT2
= 0
for c = 1 to C do
sc2
= 0
for m = 1 to
M do
if Clasa(m)
= c then
sc2
= sc2
+||x(m) – w(c)||2
sc2
= sc2
/ n(c)
sT2
= sT2
+sc2
7.
Criteriul de oprire: dacă
prototipurile s – au schimbat nesemnificativ – adică ||z(c)
– w(c)|| < e pentru toate centrele
c = 1,…, C – algoritmul se încheie. În caz contrar, se
memorează noile prototipuri:
for c = 1 to C do z(c)
= w(c)
şi se revine la pasul 4.
3. Reţele Kohonen
Teuvo
Kohonen, profesor la Universitatea Tehnică din Helsinki, este probabil
unul din cei mai faimoşi şi prolifici cercetători în domeniul
teoriei şi aplicaţiilor RNA. Dânsul a propus o varietate foarte
largă de reţele neuronale, care în ansamblu au ajuns să-i poarte
numele. Totuşi, în majoritatea cazurilor, atunci când literatura de
specialitate face referire la reţele Kohonen, se au în vedere trei
tipuri de reţele, şi anume: (a) reţeaua cuantificator
vectorial sau VQ (vector quantization); (b) reţeaua LVQ (Learning
Vector Quantization) şi (c) reţeaua pentru hărţi de
trăsături cu auto-organizare sau SOFM (Self-Organizing Feature
Maps). În lucrările sale mai sunt menţionate şi descrise
şi alte tipuri de reţele neuronale, cum ar fi: DEC (Dinamically
Expanding Context); LSM (Learning Subspace Method); ASSOM (Adaptive
Subspace Self-Organizing Maps); FASSOM (Feedback-controlled ASSOM);
LVQ-SOM ş.a.
Reţeaua SOFM – hărţi de trăsături cu auto-organizare
Hărţile
de trăsături cu auto-organizare sau, pe scurt SOFM – Self Organizing
Feature Maps – au fost inspirate din modul în care numeroase segmente
senzoriale umane sunt mapate în creier, astfel încât relaţii spaţiale
sau de alt tip între stimuli corespund unor relaţii spaţiale între
neuroni. Mai mult decât atât, cortexul cerebral poate fi comparat cu o
pânză subţire de întindere relativ mare (cca. 0.5 m2),
înfăşurată şi împăturită în forma cunoscută
doar pentru a putea ocupa spaţiul din interiorul craniului. Această „pânză”
cerebrală are anumite proprietăţi topologice remarcabile; de
exemplu, zona corespunzătoare mâinii se află lângă zona
corespunzătoare braţului, astfel încât pe această
suprafaţă bi-dimensională se realizează o proiecţie
deformată a întregului corp omenesc.
Pornind de
la aceste observaţii, Teuvo Kohonen a pus bazele teoriei
hărţilor de trăsături cu auto-organizare, care
reprezintă RNA cu învăţare nesupravegheată şi cu
ieşiri continue. Spre deosebire de marea majoritate a RNA, care au fost
dezvoltate folosind învăţarea supravegheată,
reţelele SOFM au fost concepute din start pentru învăţarea
nesupravegheată, numită uneori şi auto-organizare.
Dacă în cazul învăţării supravegheate setul de antrenare
conţine perechi intrare – ieşire dorită, iar reţeaua
trebuie să realizeze o mapare a intrărilor spre ieşiri, în cazul
auto-organizării , setul de antrenare conţine numai mărimi de
intrare. În acest caz, nu mai poate fi vorba de nici un tip de asociere intrare
– ieşire, reţeaua SOFM încercând, de fapt, să înveţe
structura datelor de intrare.
Auto-organizarea se
defineşte ca şi capacitatea unui sistem de a descoperi şi
învăţa structura datelor de intrare, chiar şi în cazul
inexistenţei vreunei informaţii despre această structură
[Kohonen 88]. Reţeaua neuronală cu auto-organizare învaţă singură,
fără a i se indica răspunsul corect pentru un model prezentat la
intrare. Într-o altă formă [Haykin 99], se poate spune că o
reţea neuronală cu auto-organizare, care foloseşte principiul
învăţării nesupravegheate, descoperă trăsături
caracteristice ale datelor de intrare, fără a folosi valori
cunoscute sau dorite la ieşire. Informaţiile privind aceste
trăsături ale datelor de intrare se creează în procesul de
învăţare şi sunt memorate în ponderile conexiunilor sinaptice,
sub forma aşa-numitelor prototipuri. În acest fel, în orice moment,
ieşirile reţelei vor descrie relaţia dintre intrarea
curentă şi prototipurile memorate în reţea.
În
funcţie de tipurile de trăsături caracteristice identificate la
nivelul datelor de intrare, se disting două grupuri de algoritme de
învăţare nesupravegheată şi reţele neuronale asociate:
(a) învăţarea hebbiană, care descoperă „forma”
datelor şi (b) învăţarea competitivă, care descoperă „organizarea”
datelor. Ultimul tip de învăţare a fost descris în cadrul acestui
capitol, iar în cele ce urmează se vor indica detalii suplimentare privind
auto-organizarea.
Învăţarea
hebbiană extrage din datele de intrare un set de direcţii
principale, în lungul cărora sunt organizate datele într-un
spaţiu p-dimensional (Fig. a). Fiecare direcţie este
reprezentată de un vector al ponderilor relevante. Numărul
direcţiilor principale este cel mult egal cu dimensiunea spaţiului
datelor de intrare, p. De exemplu, pentru cazul unui spaţiu
bi-dimensional, ca cel din Fig. a, datele sunt organizate în lungul a două
direcţii principale, notate w1 şi w2.
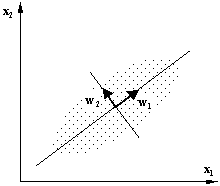
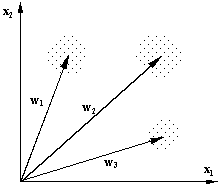
(a) (b)
Învăţarea
competitivă extrage din datele de intrare un set de prototipuri
sau vectori centru asociaţi unor zone din spaţiul datelor de intrare,
în care sunt grupate o parte dintre acestea (Fig. b). Fiecare prototip este
memorat ca un vector de ponderi. Este evident că în acest caz numărul
de prototipuri este independent de dimensiunea spaţiului de intrare.
Pentru cazul unui spaţiu bi-dimensional, cum este cel din Fig. b, datele
sunt organizate în trei zone sau nori, ale căror prototipuri sunt
reprezentate de vectorii de ponderi w1, w2
şi w3. O extindere importantă a
învăţării competitive standard este conceptul introdus de
Kohonen şi cunoscut sub numele de hărţi de
trăsături. În principiu, o hartă de trăsături se
obţine dacă la neuronii dintr-o reţea cu învăţare
competitivă se adaugă o anumită formă de organizare
topologică.
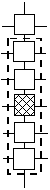
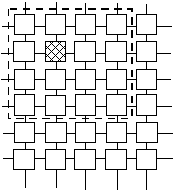
Reţeaua
SOFM foloseşte o dispunere a neuronilor în nodurile unei grile, de obicei
bi-dimensionale, dar uneori uni-dimensională sau chiar tri şi chiar
multi-dimensională. De exemplu, in figura de mai jos se indică
cazurile organizării neuronilor folosind grile uni şi
bi-dimensionale. Aşezarea neuronilor în nodurile acestei grile
caracterizează poziţiile relative ale neuronilor unul în raport cu
ceilalţi, adică proprietăţile topologice şi nu
localizarea geometrică.
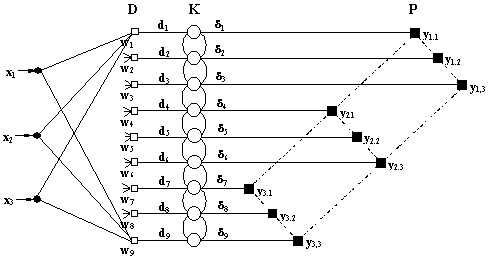
Structura
unei reţele SOFM, pentru cazul particular al unui spaţiu de intrare
cu trei dimensiuni şi al unui spaţiu al trăsăturilor
(grila-suport a neuronilor) cu două dimensiuni, este prezentat mai jos
Un neuron
din grila-suport este asociat de regulă unei clase, motiv pentru care
pentru acesta se foloseşte denumirea neuron-clasă. Fiecare
asemenea neuron-clasă este caracterizat de poziţia sa în
grila-suport, specificată de un vector cu două componente, şi de
un prototip, specificat de un vector cu trei componente:
yv = y(v1,v2) , de exemplu y1,2
wc = (w1,
c , w2, c , w3, c) pentru neuronul c
Reţeaua
SOFM are următoarea structură: (a) stratul de intrare, format
dintr-un număr de neuroni egal cu numărul dimensiunilor
spaţiului de intrare (în cazul de faţă, 3); (b)
stratul de ieşire, format din
C neuroni, dispuşi
în nodurile grilei bi-dimensionale (în cazul de faţă, C
= 9). Între stratul de intrare şi cel de ieşire se găsesc
două straturi intermediare care calculează distanţa dintre
vectorul curent x şi prototipurile existente wc
(c = 1,…,C) – stratul D – respectiv asigură
competiţia între neuroni pentru determinarea prototipului cel mai apropiat
de modelul curent – stratul K. Structura stratului competitiv K
este cea a unei reţele Max / MinNet descrise în § 8.4.1. În
straturile D şi K există C neuroni, câte unul
pentru fiecare neuron-clasă din stratul de ieşire. Prototipurile
asociate fiecărui neuron-clasă sunt memorate în ponderile
conexiunilor dintre neuronii din stratul de intrare şi stratul D.
(a) (b)
Conform
acestei arhitecturi, reţeaua SOFM este o reţea competitivă care
asigură maparea topologică, de la spaţiul de intrare, către
prototipurile spaţiului de ieşire. După prezentarea unui
număr suficient de vectori de intrare, neuronii-clasă din reţea
vor evidenţia grupări de puncte sub forma unor nori, care
partiţionează spaţiul de intrare. Totodată, reţeaua
SOFM încearcă să identifice clasele astfel încât oricare doi
neuroni-clasă învecinaţi vor avea prototipuri apropiate în
spaţiu şi care acţionează la vectori de intrare
asemănători, obţinându-se astfel o ordonare naturală a
informaţiei.
Un alt mod
de a interpreta reţeaua SOFM este următorul: reţeaua
încearcă să proiecteze grila-suport în spaţiul de
intrare, astfel încât fiecare vector de antrenare să fie cât mai apropiat
de un anumit prototip, iar proiecţia grilei-suport să fie cât mai
puţin posibil deformată.
Principala
particularitate a reţelelor SOFM constă în aceea că adaptarea
prototipurilor are loc nu numai pentru neuronul câştigător, ci
şi pentru o parte din neuronii-clasă din reţea, care se
află într-o anumită vecinătate a neuronului
câştigător. Astfel, o noţiune specifică reţelelor SOFM
este vecinătatea unui neuron-clasă c, notată Vc
şi definită ca reprezentând mulţimea neuronilor-clasă
dispuşi în nodurile grilei-suport la o distanţă faţă
de neuronul-clasă c mai mică decât o anumită valoare
prag. Vecinătatea unui neuron-clasă c include întotdeauna
şi neuronul respectiv. O vecinătate Vc este
centrată pe neuronul-clasă c, modelându-se astfel
interacţiunea laterală constatată la sistemele biologice.
Acest principiu
de adaptare a prototipurilor poate fi implementat în algoritmul de
învăţare prin înglobarea a două strategii complementare: competiţia
şi cooperarea. La nivelul unei reţele SOFM, competiţia
înseamnă că toţi neuronii-clasă concurează pentru
dreptul de a învăţa. Implementarea competiţiei se face ca în
orice alt algoritm competitiv: fiecare vector x(m) din
setul de antrenare este comparat cu prototipurile wc
asociate neuronilor-clasă şi se determină neuronul
câştigător c* şi poziţia acestuia pe grila-suport,
notată Pc*. Desigur, neuronul câştigător c*
este acela pentru care distanţa ||x(m) – wc*||
este minimă.
Cooperarea
înseamnă că, după stabilirea neuronului câştigător c*,
acesta nu îşi adaptează prototipul de unul singur, ci împreună
cu neuronii-clasă care se situează în vecinătatea sa Vc*.
În ceea ce priveşte vecinătatea unui neuron, aceasta poate fi
definită, în principiu, sub două forme: discretă şi
continuă. În cazul vecinătăţilor discrete, se folosesc
direct valori întregi; de exemplu, avem de a face cu o vecinătate a
neuronului central egală cu 2 (dacă neuronul central se află
spre extremitatea grilei-suport, în zona respectivă se vor include în
vecinătatea sa numărul maxim de neuroni posibil – câte un neuron-clasă).
Pentru vecinătăţile continue se foloseşte o funcţie de
vecinătate, având de regulă o formă gaussiană:
unde s 2 este
parametrul dispersie, care descrie împrăştierea
distribuţiei gaussiene, iar rc este distanţa dintre
neuronul-clasă c şi neuronul câştigător c*,
măsurată prin diferenţa dintre poziţiile celor doi neuroni
pe grila-suport:
rc = | Pc
– Pc* |
De fapt,
pentru cazul continuu, vecinătatea neuronului câştigător c*
este definită de parametrul împrăştiere s 2. Astfel,
cu cât gradul de împrăştiere s 2 pentru
neuronul câştigător c* este mai mare, cu atât vecinătatea
sa va fi mai largă. În practică, vecinătăţile continue
se folosesc după următorul model: pentru valoarea curentă a gradului
de împrăştiere s 2 se
calculează valorile funcţiei de vecinătate Vc,
folosind relaţia (8.60), pentru toţi neuronii-clasă,
distanţele acestora faţă de neuronul câştigător c*
fiind calculate cu relaţia de mai sus. Toţi neuronii c, pentru
care valoarea astfel calculată Vc este mai mică sau
egală cu o valoare prag impusă, vor intra în vecinătatea
neuronului câştigător c*.
Algoritmul
de învăţare al reţelei SOFM urmăreşte formarea
hărţii de trăsături care să surprindă
caracteristicile esenţiale ale datelor din setul de antrenare şi
să proiecteze aceste caracteristici în spaţiul grilei-suport.
În acest scop, se porneşte de la prototipurile asociate fiecărui
neuron-clasă care sunt iniţializate aleatoriu, cu valori mici, în
intervalul (0 , 1). În continuare, se consideră succesiv fiecare model de
antrenare x(m), pentru care urmează să se
adapteze prototipurile neuronilor-clasă. Problema adaptării
prototipurilor poate fi abordată, în principiu, pe două căi,
vorbindu-se despre adaptarea unilaterală, respectiv adaptarea
bilaterală. În cazul adaptării unilaterale, după
determinarea neuronului câştigător c*, se face adaptarea
ponderilor numai pentru neuronii din vecinătatea Vc*,
prin apropierea prototipurilor acestora de modelul curent x(m).
Restul neuronilor îşi păstrează prototipurile nealterate.
Formal, se poate scrie:
wc = wc + h × (x(m)
– wc ) c
Î Vc*
wc = wc
c
Ď Vc*
În cazul
adaptării bilaterale, se aplică o strategie dublă:
neuronii-clasă din vecinătatea neuronului câştigător sunt stimulaţi,
astfel încât prototipurile lor sunt adaptate pozitiv, în sensul apropierii de
modelul curent; pe de altă parte, neuronii-clasă care rămân în
afara vecinătăţii neuronului câştigător sunt penalizaţi,
astfel încât prototipurile lor sunt adaptate negativ, în sensul îndepărtării
de modelul curent. Pentru acest caz, legea de adaptare a prototipurilor are
forma:
wc = wc + h+ × (x(m)
– wc ) c
Î Vc*
wc = wc
– h– × (x(m)
– wc ) c
Ď Vc*
Mărimile h, h+ şi h– au
semnificaţiile unor rate de învăţare.
În
contextul adaptării dimensiunilor vecinătăţilor, în
procesul de antrenare se disting două faze sau etape, şi anume: (a) etapa
de ordonare şi (b) etapa de convergenţă. În etapa de
ordonare, când se folosesc vecinătăţi largi, are loc organizarea
grosieră a hărţii de trăsături şi ordonarea
primară a caracteristicilor datelor de intrare. În cursul etapei de
convergenţă, când are loc diversificarea prototipurilor neuronilor-clasă, vecinătăţile
se îngustează treptat, până la 0.
În cazul
în care se folosesc vecinătăţi continue, dimensiunea acestora
este controlată prin valoarea gradului de împrăştiere s 2.
Iniţial, parametrul s 2 are
valori mari, astfel încât vecinătatea oricărui neuron include practic
întreaga reţea. În cursul etapei de ordonare, s 2 se reduce
treptat, pentru a include doar câţiva neuroni-clasă din imediata
vecinătate a neuronului câştigător. În final, în cursul etapei
de convergenţă, dispersia s 2 se anulează,
astfel încât – conform relaţiei (8.60) – vecinătatea fiecărui
neuron se reduce la 0, adică la el însuşi.
Alături
de dimensiunea vecinătăţilor, un alt factor care
influenţează hotărâtor convergenţa procesului de
învăţare este rata de învăţare, h. Şi
pentru acest parametru se foloseşte o strategie de descreştere în
timp. Iniţial, în faza de ordonare, rata de învăţare se
menţine la valori ridicate, apropiate de unitate, pentru a permite
orientarea de principiu a tuturor prototipurilor din reţea către diferitele
modele din setul de antrenare. Ulterior, în etapa de convergenţă,
când modificarea prototipurilor trebuie să se facă în zone din ce în
ce mai apropiate de centrul grupării de vectori asociaţi unui
neuron-clasă, rata de învăţare trebuie redusă până la
valori suficient de mici, de exemplu 0.1.
Forma de
principiu a algoritmului de învăţare pentru reţeaua SOFM, în
ipoteza unor vecinătăţi continue şi fără valoare
prag a vecinătăţii, este prezentată mai jos. În
comparaţie cu tipurile de vecinătăţi descrise deja
(discrete şi continue), algoritmul utilizează un tip special de
vecinătăţi continue, care nu mai sunt controlate de o valoare
prag impusă. În acest caz, se foloseşte direct valoarea funcţiei
de vecinătate, calculată cu relaţia (8.60), care afectează
rata de învăţare h. Cu cât
neuronul-clasă c este
mai îndepărtat pe
grila- suport de neuronul câştigător c* (distanţa rc este mai
mare), cu atât funcţia de vecinătate a primului neuron este mai
mică şi, în consecinţă, cu atât modificarea prototipului wc
este de mai mică amploare.
Algoritmul
de învăţare pentru reţeaua SOFM.
1. Date de
intrare: modelele de antrenare, sub forma vectorilor de intrare x(m),
m = 1,…,M; numărul de neuroni-clasă C; rata de
învăţare h şi
dispersia s 2; factorii
de descreştere pentru rata de învăţare (dh) şi
dispersie (ds).
2. Iniţializarea
prototipurilor reţelei cu valori aleatorii, în intervalul (0 , 1):
for c = 1 to C do
wc
= random( )
3. Adaptarea
prototipurilor neuronilor-clasă:
for m = 1 to M do
// Calculul distanţelor dintre modelul x(m)
şi prototipurile wc
for c = 1 to C do
Dm,c = || x(m)
– wc ||
//
Selectarea neuronului-clasă câştigător
Dmin = Dm,1;
c* = 1;
for c = 2 to C do
if Dm,c < Dmin then
Dmin = Dm,c
c* = c
// Calculul funcţiei de
vecinătate pentru toţi neuronii-clasă
for c = 1 to C do
if c ą c*
then 
// Adaptarea prototipurilor
for c = 1 to C do
wc = wc
+ h× Vc
× ( x(m)
– wc )
4. Criteriul
de oprire: dacă condiţia de oprire este satisfăcută,
algoritmul se încheie. În caz contrar, se trece la pasul 5.
5. Îngustarea
vecinătăţilor în etapa de ordonare:
s 2 = s 2 × ds
6. Reducerea
ratei de învăţare în etapa de convergenţă:
h = h × dh
7. Se revine la pasul 3.
Pe de
altă parte, se constată că algoritmul din Caseta 8.13
foloseşte adaptarea unilaterală, corecţiile tuturor
prototipurilor făcându-se într-un
singur sens, către apropierea de modelul de antrenare curent x(m).
Dacă se doreşte utilizarea adaptării bilaterale, este
necesară precizarea în datele de intrare a unei vecinătăţi
critice V* şi înlocuirea codului din zona de adaptare a ponderilor
cu:
for c = 1 to C
do
if Vc > V* then wc
= wc + h× Vc
× ( x(m)
– wc )
else wc = wc – h× Vc
× ( x(m)
– wc )
Dacă
se procedează în acest fel, pentru toţi neuronii-clasă a
căror funcţii de vecinătate Vc
depăşeşte valoarea critică V* (sunt suficient de
apropiaţi de neuronul câştigător) se aplică adaptarea
pozitivă, prin apropierea prototipurilor de modelul curent x(m).
Dimpotrivă, pentru neuronii-clasă cu funcţii de vecinătate Vc
sub valoarea critică V* (care sunt suficient de depărtaţi
de neuronul câştigător), adaptarea se face în sens invers, prin
îndepărtarea prototipurilor de modelul de antrenare curent x(m).
Algoritmul
standard de învăţare pentru reţelele SOFM prezintă o serie
de neajunsuri, dintre care menţionăm: (a) caracterul preponderent
euristic, deoarece criteriul de oprire nu are la bază optimizarea unui
proces sau a datelor (algoritmul se întrerupe chiar dacă vectorii
soluţie obţinuţi nu sunt optimi); (b) prototipurile finale
asociate fiecărui neuron-clasă depind de iniţializarea
reţelei şi de ordinea de prezentare a modelelor de antrenare; (c)
strategia de adaptare a parametrilor de învăţare h şi s 2 este, de
regulă, dependentă de problemă.
O parte
din aceste neajunsuri pot fi eliminate prin incorporarea în algoritmul de
învăţare a tehnicilor fuzzy, care permit definirea unei probleme de
optimizare pentru strategia de învăţare [Dumitrescu şi Costin
96]. În acest caz, adaptarea prototipurilor se face după o relaţie de
principiu, de forma:
wc = wc
+ qm,c × ( x(m)
– wc )
unde qm,c = qc(x(m))
(c = 1,…,C şi m = 1,…,M) sunt C
mulţimi fuzzy ce formează o partiţie fuzzy a setului de date de
antrenare X = { x(1), x(2),…, x(M)
}. Coeficienţii qm,c se calculează cu relaţia:
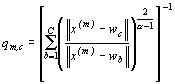
iar cu ajutorul lor se determină câte o rată de
învăţare hm,c,
asociată fiecărui model de antrenare m şi fiecărui
neuron-clasă c:
unde Tmax este
numărul maxim de iteraţii, iar a şi b sunt
parametri reali supraunitari.
Calculul
unor rate de învăţare distincte pentru fiecare model de antrenare m
şi fiecare neuron-clasă c face posibilă adoptarea unei
strategii de antrenare pe întregul lot. Astfel, adaptarea prototipurilor nu se
mai face după prezentarea fiecărui model de antrenare, ci o
singură dată, după prezentarea tuturor modelelor şi
calculul ratelor de învăţare hm,c conform regulii:
wc = wc
+ 
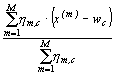c = 1,…,C
Adoptarea acestei strategii de
antrenare pe întregul lot elimină practic dependenţa rezultatelor
clasificării de ordinea de prezentare a modelelor de antrenare.
Algoritm
hibrid SOFM – fuzzy.
1. Date de
intrare: modelele de antrenare, sub forma vectorilor de intrare x(m),
m = 1,…,M; numărul de neuroni-clasă C;
parametrii a, b şi Tmax.
2. Iniţializarea
prototipurilor reţelei cu valori aleatorii, în intervalul (0 , 1):
for c = 1 to C do
wc =
random( )
3. Iniţializarea
contorului de iteraţii: t = 1.
4. Adaptarea
prototipurilor neuronilor-clasă în iteraţia curentă:
// Calculul ratelor de învăţare
for m = 1 to M do
for c
= 1 to C do
q = 0
for b = 1 to C do
q = q + || x(m) – wb
|| – 2/(a – 1)
q = || x(m)
– wc || – 2/(a – 1) × q
– 1
hm,c = q(b – 1) /
Tmax
//
Memorare prototipurilor
for c = 1 to C do Twc
= wc
// Adaptarea prototipurilor
for c = 1 to C do
S1 = 0; S2
= 0;
for m = 1 to M do
S1 = S1
+ hm,c × ( x(m)
– wc )
S2 = S2
+ hm,c
wc = wc
+ S1 / S2
5. Criteriul
de oprire: abaterea maximă dintre prototipuri.
Dacă maxc
= 1,…,C ( || Twc – wc
|| ) < e,
algoritmul se încheie. În caz contrar, se trece la pasul 6.
6. Incrementarea
contorului de iteraţii: t = t + 1. Dacă t > Tmax,
algoritmul se încheie. În caz contrar se revine la pasul 4.