Studii de profilare a sarcinii – modelarea consumatorilor din reţelele de distribuţie

Din punct de vedere istoric, standardele de măsurare şi facturare au la bază consumul total de energie electrică din perioada de facturare, iar marilor consumatori comerciali şi industriali li se aplică aşa-numitele tarife binome. Cu excepţia marilor consumatori industriali, la care grupurile de măsură sunt prevăzute cu posibilitatea înregistrării curbei de sarcină, pentru restul consumatorilor procedura standard furnizează puterea maximă absorbită şi consumul total de energie, fără nici o indicaţie privind modul în care este consumată energia respectivă în diferite ore şi zile.

Schimbările care se înregistrează în prezent în sectorul energetic şi evoluţia pieţei de energie electrică au adus în actualitate problema dezvoltării unor modele care să permită participarea la piaţă a tuturor consumatorilor. Aceste modele sunt esenţiale, mai cu seamă în cazul consumatorilor casnici şi comerciali, care reprezintă majoritatea clienţilor companiilor de electricitate şi pentru care o campanie de instalare a contoarelor electronice s-ar dovedi extrem de costisitoare şi probabil total neeconomică. Pentru aceşti consumatori soluţia alternativă este utilizarea în continuare a contoarelor tradiţionale şi estimarea unor curbe de sarcină profilate orar, care să stea la baza închiderii balanţelor orare şi a facturării şi, pe această cale, să permită participarea acestor consumatori la piaţa de energie electrică.

În acest context, tehnicile de profilare a sarcinii reprezintă un set de proceduri care permit transformarea istoricului de consum al unor consumatori, care nu sunt echipaţi cu contoare electronice, într-o serie de curbe de sarcină estimate, pentru categoria respectivă de consum, profilate orar, denumite frecvent grafice sau curbe tip de sarcină. Sintagma „profilarea sarcinii” se referă cu precădere la utilizarea acestor grafice tip de sarcină în cadrul unor proceduri speciale legate de tranzacţiile cu energie electrică şi decontările între actorii pieţei.

Dintre tehnicile de profilare a sarcinii folosite în prezent, majoritatea lucrărilor care abordează problematica profilării sarcinii recomandă profilarea statică ajustată ca fiind cea mai eficientă în momentul de faţă. Această tehnică de profilare extrage curbele tip de sarcină prin prelucrarea istoricului de date pentru o anumită categorie de consum, care sunt apoi ajustate pentru a reflecta influenţa anumitor factori (de exemplu, condiţiile meteorologice).

Una dintre cele mai sensibile etape în raport cu rezultatele profilării este segmentarea. În cursul acestei etape se stabileşte numărul de grafice tip de sarcină ce urmează să descrie consumatorii din categoriile reprezentative pentru populaţia considerată. În general, ca parametri de segmentare se pot folosi individual sau în combinaţii: activitatea desfăşurată de consumator; amplasarea acestuia în cadrul sistemului; tariful aplicat; nivelul de consum, apreciat după puterea absorbită, energia consumată sau factorul de putere; tipul zilei şi sezonul.

În ceea ce priveşte aplicaţiile IA în profilarea sarcinii, există deja o serie de studii care evidenţiază posibilitatea utilizării modelelor cu auto-organizare (reţele Kohonen) în prognoza pe termen mediu a consumului de energie electrică. Alte studii ilustrează posibilitatea aplicării aceloraşi modele de auto-organizare pentru extragerea graficelor tip şi clasificarea ulterioară a consumatorilor pe baza acestor grafice tip cu ajutorul reţelelor Hopfield.

Utilizarea auto-organizării în procesul de profilare a sarcinii are avantajul de a permite desfăşurarea simultană a etapelor de segmentare şi construire a curbelor tip de sarcină. Suprapunerea acestor etape are efecte benefice asupra profilării în general, în sensul în care elimină riscul asocierii unui grafic de sarcină măsurat unei clase de consum eronate. Procesul de segmentare se poate desfăşura automat, fără a necesita intervenţia operatorului uman. De asemenea, separarea unor curbe tip de sarcină distincte pentru zilele lucrătoare şi cele de repaus se desfăşoară automat în cadrul procesului de auto-organizare şi are loc numai atunci când formele curbelor de sarcină măsurate impun această distincţie.

În contextul profilării sarcinii au fost testate diferite variante de implementare a auto-organizării în reţele Kohonen, cum ar fi algoritmul de auto-organizare standard, algoritmul de auto-organizare cu creşterea reţelei şi o variantă a acestuia care foloseşte principiul de ponderare după orele de vârf şi/sau de gol de sarcină şi algoritmul de auto-organizare cu învăţare fuzzy. Cele mai bune rezultate au fost obţinute în cazul implementării fuzzy a principiului de auto-organizare, care are şi marele avantaj de a elimina influenţa pe care o are procesul de iniţializare asupra rezultatelor clasificării.

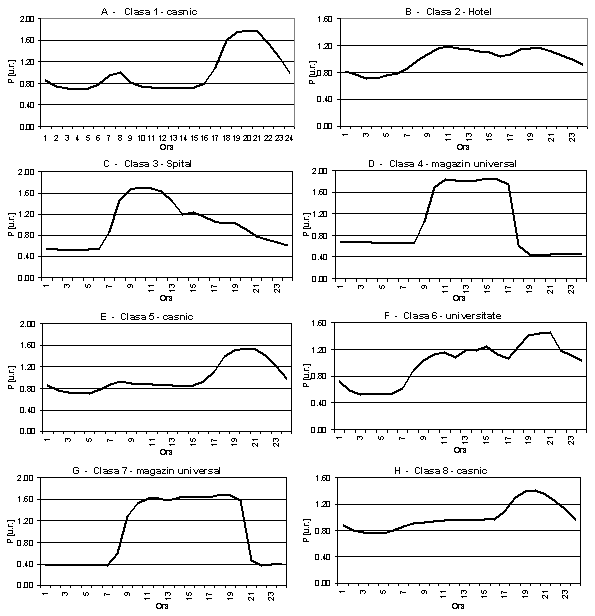
Astfel, folosind o bază de date formată din 97 grafice zilnice măsurate în 11 posturi de transformare care alimentează grupuri omogene de consumatori (din categoriile casnic, spital, hotel, magazin universal, universitate) şi o reţea Kohonen cu 8 neuroni-clasă (corespunzători la 8 segmente de consum), au fost separate graficele tip de sarcină prezentate mai jos.

De asemenea, în tabelul de mai jos se indică rezultatele procesului de clasificare, sub forma numărului de grafice aparţinând diferitelor categorii de consumatori care au fost asociate celor 8 clase. În final, asocierea clasei la o categorie de consum se face pe baza numărului maxim de clasificări din tabel.

		Consumatori											Tipul clasei
		1	2	3	4	5	6	7	8	9	10	11
Clase	1	0	0	0	0	0	0	0	7	0	0	0	Casnic 1
	2	1	2	6	6	0	0	0	0	0	0	0	Hotel
	3	9	5	0	0	1	0	0	0	0	0	0	Spital
	4	0	0	0	0	1	0	0	0	0	0	0	Magazin universal – zi repaus
	5	0	0	0	0	0	0	7	1	0	0	10	Casnic 2
	6	0	0	0	1	0	9	0	0	0	0	0	Universitate
	7	0	0	0	0	6	0	0	0	0	0	0	Magazin universal – zi lucrătoare
	8	0	0	1	0	0	0	1	0	11	11	1	Casnic 3

Analiza curbelor din evidenţiază faptul că în cazul consumatorilor casnici au fost izolate 3 curbe tip distincte, dar nici una dintre acestea nu descrie separat zilele lucrătoare şi cele de repaus (A, E şi H). Deosebirile marcante dintre aceste curbe se referă atât la nivelul diferit de consum în perioada orelor de vârf, cât şi la forma curbelor de sarcină în zona golului de după-amiază. Pe de altă parte, se observă că modelul de auto-organizare a extras curbe tip de sarcină distincte pentru zilele lucrătoare şi cele de repaus pentru un singur consumator, şi anume magazinul universal (D şi G). Pentru restul consumatorilor monitorizaţi, deosebirile între graficele de sarcină măsurate pentru cele două tipuri de zile sunt neesenţiale şi, ca urmare, nu au fost extrase curbe tip distincte.

Tehnicile de profilare a sarcinii şi rezultatele furnizate de acestea (graficele tip de sarcină) pot fi utilizate într-o gamă largă de aplicaţii, cum ar fi: (i) administrarea activităţii consumatorilor şi asistenţă tehnică acordată acestora; (ii) promovarea şi aplicarea unor strategii DSM; (iii) dezvoltarea şi implementarea unor noi tarife; (iv) identificarea şi promovarea unor noi tipuri de servicii; (v) exploatarea eficientă a reţelelor de distribuţie; (vi) furnizarea unor prognoze pe termen scurt şi mediu; (vii) planificarea activităţii de achiziţie a energiei electrice de către furnizori.

Studii de profilare a sarcinii – identificarea consumatorilor din reţelele de distribuţie

Procesul de clasificare prin auto-organizare descris în paragraful anterior se încheie prin extragerea unor grafice tip de sarcină, care sunt asociate anumitor categorii de consumatori. La finalul acestui proces, reţeaua Kohonen poate fi folosită pentru asocierea unui grafic măsurat la o categorie sau segment de consum. În acest scop, pe intrarea reţelei se aplică valorile orare ale graficului de sarcină măsurat, iar reţeaua calculează „distanţele” dintre acest grafic şi graficele tip memorate şi – prin intermediul unei sub-reţele MaxNet – selectează neuronul-clasă „câştigător”, cel al cărui grafic tip se apropie cel mai mult de forma graficului de sarcină măsurat. Acest proces poartă numele de identificarea sau recunoaşterea tiparului de consum.

Aceeaşi sarcină poate fi încredinţată unui alt tip de RNA specializată în recunoaşterea formelor, şi anume reţeaua Hopfield. Deoarece reţeaua Hopfield foloseşte pe intrări şi ieşiri mărimi binare (±1), pentru reprezentarea graficelor tip de sarcină se folosesc câte 7 neuroni pentru fiecare palier orar (în total 168 neuroni), iar valorile sarcinilor sunt convertite în reprezentare binară, folosind –1 în loc de 0. Pentru valorile uzuale din graficele tip de sarcină această reprezentare asigură o precizie suficient de bună, erorile de conversie nedepăşind 2%.

După antrenare, reţeaua Hopfield poate fi folosită în două tipuri de aplicaţii: (a) filtrare: stabilirea corespondenţei dintre un grafic de sarcină înregistrat în reţea şi unul din graficele tip memorate; (b) completare: stabilirea corespondenţei dintre un grafic de sarcină înregistrat, pentru care o parte din valorile palierelor orare sunt afectate de perturbaţii majore, şi unul din graficele tip memorate. Pentru amândouă tipurile de aplicaţii, reţelei Hopfield i se prezintă, pe intrare, graficul măsurat şi se aplică un proces iterativ, până când în doi paşi succesivi ieşirile reţelei nu se mai modifică. În acest moment, valorile de pe ieşirile reţelei Hopfield descriu graficul tip de sarcină identificat.

De exemplu, pentru o aplicaţie de filtrare, reţeaua Hopfield recunoaşte graficul tip asociat pentru abateri absolute procentuale la nivelul unui palier orar de până la 7%. Identificarea categoriei de consum, în sensul stabilirii unui grafic tip de sarcină care se apropie cel mai mult de graficul măsurat pentru un anumit consumator, se realizează însă în condiţiile unor abateri mult mai mari la nivelul palierelor orare, aşa cum este ilustrat în figura. În această figură se indică graficele măsurat şi recunoscut pentru cazul a doi consumatori care au fost clasificaţi în categoriile casnic, respectiv, spital.

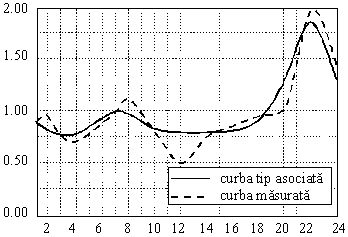
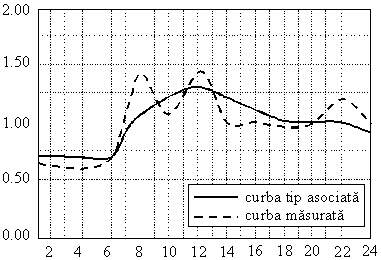
(a) (b)

Identificarea categoriei de consum prin filtrare pentru un consumator casnic (a) şi un consumator de tip spital (b).

În cazul aplicaţiilor de tip completare, reţeaua Hopfield recunoaşte graficul tip de sarcină, chiar în absenţa unui număr de până la 10 valori ale palierelor orare (în acest caz, totuşi, este necesar ca valorile cunoscute să corespundă unor paliere care individualizează graficul tip respectiv printre celelalte grafice tip memorate).

Tot în categoria aplicaţiilor de identificare a sarcinii intră şi problemele care urmăresc stabilirea structurii de consum a unei sarcini complexe, în componenţa căreia intră consumatori aparţinând unor categorii de consum diferite. Se urmăreşte de fapt, descompunerea unui grafic de sarcină măsurat în mai multe grafice de sarcină corespunzătoare fiecărei categorii de consum cunoscute. În acest caz se aplică un model matematic tradiţional de tipul celor mai mici pătrate.

Pornind de la graficul de sarcină înregistrat în nodul cu sarcină complexă y şi matricea graficelor tip de sarcină G, se urmăreşte într-o primă etapă determinarea coeficienţilor de transformare din vectorul a care realizează trecerea de la graficele tip de sarcină exprimate în unităţi relative, la graficele de sarcină asociate fiecărei categorii de consum, exprimate în unităţi absolute ŷ_i. Determinarea coeficienţilor a_i se face prin rezolvarea sistemului de ecuaţii liniare:

G^T × G × a = G^T × y

iar contribuţia fiecărui consumator tip la formarea graficului total de sarcină măsurat rezultă ca:

ŷ_i = a _i × g _i i=1,…,N

Din punct de vedere matematic, problema considerată este echivalentă cu descompunerea vectorului y după N vectori g _i şi admite soluţie unică numai dacă vectorii g _i sunt liniari independenţi – adică nici unul din ei nu poate fi exprimat ca o combinaţie liniară a celorlalţi. Altfel spus, fiecare grafic tip de sarcină din baza de date trebuie să fie de sine stătător. Pe de altă parte, rezolvarea sistemului de ecuaţii liniare nu conduce întotdeauna la soluţii fezabile. De exemplu, o soluţie care conţine unul sau mai mulţi coeficienţi a_i negativi nu are sens în practică. De aceea, rezolvarea problemei descrise de acest sistem trebuie corelată cu o restricţie de forma a _i ³ 0, i=1,…,N.

Reprezentarea sarcinii în studiile de stabilitate (RNA)

În prezent, cele mai răspândite modele de sarcină utilizate în studiile de stabilitate folosesc fie agregarea unor componente individuale, fie estimări pe baza teoriei identificării sistemelor. Ambele abordări prezintă anumite neajunsuri, care pot fi depăşite în cazul folosirii unor modele bazate pe RNA. Astfel, propune tocmai o asemenea abordare, care foloseşte două tipuri de reţele neuronale, şi anume reţelele cu conexiuni funcţionale (FLN) şi reţelele polinomiale.

Utilizarea reţelelor cu conexiuni funcţionale are, în primul rând, avantajul de a nu folosi neuroni ascunşi, ceea ce determină timpi de antrenare foarte reduşi. De exemplu, reţelele FLN pot aproxima variaţia sarcinii în timp ca urmare a variaţiilor de tensiune şi/sau frecvenţă. Astfel, în figura se indică arhitectura de principiu a unei reţele FLN, care calculează variaţia puterii active la momentul k în funcţie de variaţiile aceleiaşi mărimi şi a tensiunii la momente anterioare k-l şi k-m, exprimate direct şi sub formă funcţională (în acest exemplu se folosesc funcţiile trigonometrice sin şi cos).

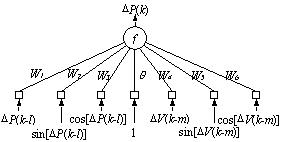
Reţea FLN cu intrări funcţionale.

Pe de altă parte, reţelele polinomiale au, în general, o structură foarte asemănătoare cu cea a Perceptronului Multistrat, însă folosesc ca funcţii de activare expresii polinomiale de diferite ordine. De exemplu, pentru un polinom de ordin doi, dacă neuronul are o intrare x_i, funcţia de activare va fi:

F = A+Bž x_i+Cž x_i²

iar în cazul a două intrări x_i şi x_j:

F = A+Bž x_i+Cž x_j+Dž x_i²+Ež x_j²+Fž x_iž x_j

Arhitectura unei reţele polinomiale se stabileşte în cursul procesului de antrenare, fiind posibilă eliminarea intrărilor nesemnificative şi utilizarea unei reţele de complexitate cât mai redusă. Astfel, în [da Silva 97] se poate folosi un algoritm de antrenare specific, cunoscut sub numele de GMDH (Group Method of Data Handling – Prelucrarea datelor cu metode de grupare), care permite construirea straturilor, unul câte unul, începând cu stratul de intrare. Acest algoritm foloseşte un set de date format din N perechi de modele intrare – ieşire dorită. Dintre aceste modele, N₁ formează setul de antrenare, iar restul de N₂ = N – N₁, formează setul test.

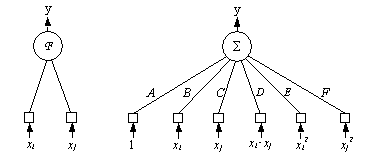
(a) (b)

Reprezentări ale neuronului în cadrul unei reţele polinomiale.

Modul de aplicare a algoritmului GMDH este ilustrat în continuare pentru cazul unui model polinomial de ordin II, care foloseşte neuroni ce primesc pe intrare câte două componente ale modelului de intrare x, fie acestea x_i şi x_j (Fig. b). Dacă vectorul de intrare x are n = K₀ componente de forma x_i, x_j primul strat va conţine K_1,0 = neuroni, fiecare asemenea neuron generând o ieşire de forma:

y = F( x_i, x_j) i, j = 1,…,n i ¹ j

unde F este polinomul din relaţia (14.6), pentru care coeficienţii A, B, C, D, E şi F se calculează ca şi ponderile unei reţele neuronale cu modelele de intrare - ieşire (x_m , y_m) m = 1,…,N₁. Folosind ieşirile calculate y_m şi valorile lor dorite d_m, se evaluează abaterile pătratice relative pentru fiecare neuron k din stratul curent:

care se ordonează crescător şi se selectează primii K₁ neuroni din această listă ordonată (K₁ este un parametru de tip prag, care se alege cu restricţia K₁ £ K_1,.0). restul de K_1,.0 – K₁ neuroni din stratul curent sunt eliminaţi.

În continuare, se generează următorul strat, care va conţine K_2,0 = neuroni şi, pentru fiecare neuron se construieşte funcţia de activare:

z = F( y_i , y_j) i, j = 1,…,K₁ i ¹ j

calculând alţi coeficienţi A, B, C, D, E şi F şi estimând alte abateri:

Se realizează din nou ordonarea neuronilor din stratul curent, crescător după valorile acestor abateri şi se selectează primii K₂ neuroni din această listă. Procesul continuă până când abaterea minimă calculată pentru stratul curent devine mai mare decât abaterea minimă calculată pentru stratul anterior. Soluţia finală corespunde reţelei neuronale care are ca neuron de ieşire neuronul cu valoarea minimă a abaterii e _k din penultimul strat. Evoluţia acestui proces este descrisă şi în figura, pentru cazul particular: n = K₀ º K₁ º K₂º K₃ = 4. În această figură pătratele reprezintă neuronii de intrare, cercurile negre – neuronii generaţi şi reţinuţi, iar cercurile albe – neuronii generaţi şi eliminaţi în procesul de creare a reţelei.

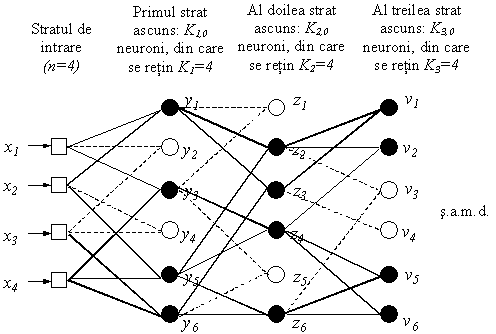
Utilizarea împreună a celor două tipuri de reţele neuronale elimină neajunsurile fiecăreia dintre ele (selectarea funcţiilor neliniare prin încercări, în cazul reţelelor FLN, respectiv riscul oscilaţiilor, în cazul reţelelor polinomiale) şi aduce o serie de noi avantaje, cum ar fi: arhitectura RNA este definită automat în procesul de antrenare, nu există parametri de antrenare ale căror valori ar trebui setate a priori, dispare problema minimelor locale şi se asigură o convergenţă rapidă.

Modelul descris a fost folosit pentru descrierea comportării unui sistem la perturbaţii de tensiune şi frecvenţă. Dintre modelele descrise în , cea mai bună comportare a avut-o modelul combinat al reţelelor FLN şi polinomiale. De exemplu, în figura se indică formele de variaţie în timp ale puterii reactive în cazul unei perturbaţii de tensiune [da Silva 97]. Corespunzător curbelor din figura, pentru cazul utilizării modelului neuronal eroarea medie este de 2,31 %, iar eroarea maximă absolută este de 15,74 %. De asemenea, în figura se indică alte două curbe, corespunzătoare altor două modele de estimare a variaţiei puterii absorbite.

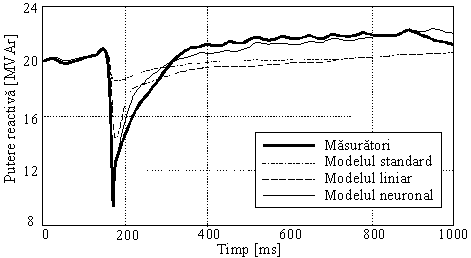
Variaţia în timp a puterii reactive pentru o perturbaţie de tensiune.

*

* *

Un alt model ce poate fi folosit pentru reprezentarea dinamică a sarcinii foloseşte o RNA recurentă. La baza utilizării acestui tip de reţele neuronale stă legătura care se admite că există între puterea activă dintr-un nod la un moment dat P(k+1), şi valorile anterioare ale puterii P(k), P(k-1) … etc, respectiv tensiunii V(k+1), V(k), V(k-1) … etc, în acelaşi nod, de exemplu:

P(k+1) = f [P(k), P(k-1), P(k-2), V(k+1), V(k)]

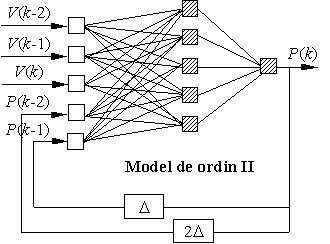
Astfel, în funcţie de ordinul modelului {P(k)}, {P(k), P(k-1)}, {P(k), P(k-1), P(k-2)}, … etc, se pot folosi RNA recurente cu arhitecturi de tipul celor prezentate în figura.

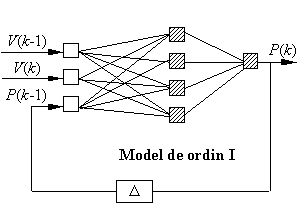
(a) (b)

Reprezentarea dinamică a sarcinii cu modele de RNA recurente de ordin I (a) şi II (b).

Pentru evaluarea performanţelor modelelor de mai sus s-a considerat o perturbaţie de tensiune şi s-a determinat răspunsul sistemului sub formă de putere activă, care s-a comparat apoi cu valorile măsurate (vezi figura de mai jos). Analiza realizată a arătat că ambele modele aproximează cu precizii comparabile răspunsul sistemului la o perturbaţie de tensiune. Erorile maxime procentuale în valoare absolută pentru cele două modelesunt de 10.3%, respectiv 8.7%, apreciându-se că utilizarea unui model de ordin 2 este suficientă .

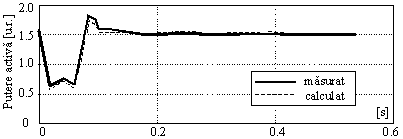
Variaţia puterii active la o perturbaţie de tensiune.