Lucrarea 3. Criteriul de aproximare dupa cele mai mici patrate: regresia polinomiala si regresia liniara
Tema A - Regresia polinomiala Tema B - Regresia liniara Tema C - Regresia parabolica
Criteriul de aproximare prin interpolare
determina functia aproximant F(x) impunand conditia ca aceasta sa
coincida cu functia de aproximat f(x) in toate nodurile de interpolare.
In felul acesta, curba asociata functiei F(x) este fortata sa urmeze
o traiectorie impusa de pozitia nodurilor de interpolare. Acest criteriu
este insa prea putin eficient in cazul unui numar mare de noduri
de
Pentru formalizarea acestui criteriu, se considera functia sub forma tabelara,
avand n+1 masuratori (x_k, f_k) afectate de erori inerente
si se urmareste determinarea unei functii de aproximare F(x), astfel
definita incat suma patratelor abaterilor in punctele de definitie sa fie
minima:
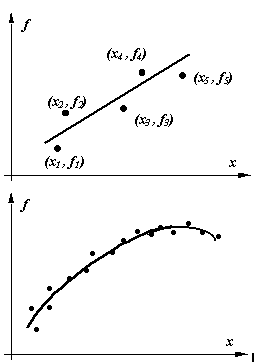 interpolare,
deoarece determinarea coeficientilor polinomului de aproximare necesita
un volum mare de calcul si exista riscul aparitiei oscilatiilor
intre noduri. In plus, daca insesi valorile indicate pentru functia f(x)
nu sunt exacte, provenind de exemplu din masuratori afectate de erori,
nu are sens sa impunem replicarea lor de catre functia de aproximare. In
aceste situatii este convenabila aplicarea unei metode care sa determine
cea mai "buna" functie care sa minimizeze abaterea medie patratica intre
f(x) si F(x) in toate punctele in care se cunoaste
valoarea functiei originare.
interpolare,
deoarece determinarea coeficientilor polinomului de aproximare necesita
un volum mare de calcul si exista riscul aparitiei oscilatiilor
intre noduri. In plus, daca insesi valorile indicate pentru functia f(x)
nu sunt exacte, provenind de exemplu din masuratori afectate de erori,
nu are sens sa impunem replicarea lor de catre functia de aproximare. In
aceste situatii este convenabila aplicarea unei metode care sa determine
cea mai "buna" functie care sa minimizeze abaterea medie patratica intre
f(x) si F(x) in toate punctele in care se cunoaste
valoarea functiei originare.
Apreciati si dvs. cum ar arata curbele ce ar descrie functia F(x)
pentru punctele de definitie din figurile alaturate daca s-ar folosi criteriul
de aproximare prin interpolare.
Aproximarea dupa criteriul celor mai mici patrate determina o functie F(x)
care nu mai trece prin punctele de definitie, ci printre
ele, astfel incat suma patratelor abaterilor intre functiile F(x)
si f(x) in aceste puncte sa fie minima.
In functie de forma functiei de aproximare F(x) pot fi aplicate mai multe tipuri de regresie: polinomiala, exponentiala, logaritmica, hiperbolica, etc.
Pentru functia tabelara considerata, regresia polinomiala foloseste o functie de aproximare de forma unui polinom de grad p, in general diferit de n :
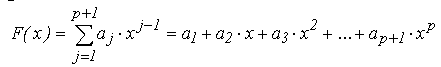
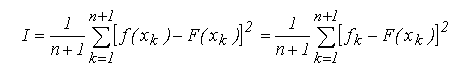
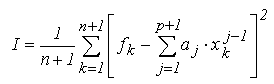
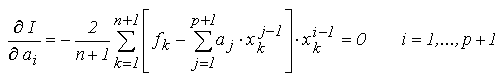
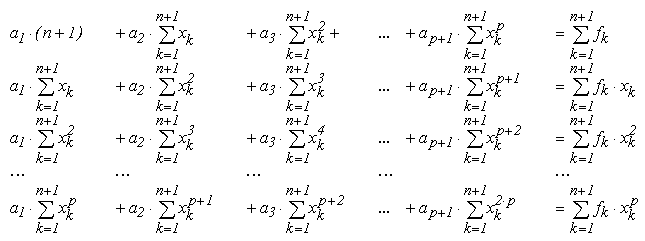
Algoritmul 1 - Aproximarea functiilor prin regresie polinomiala
- Definirea functiei tabelare: numarul punctelor cunoscute n+1, valorile nodurilor de interpolare x_k si ale functiei aproximate f_k(k=1,..., n+1).
- Definirea gradului polinomului de regresie p.
- Formarea matricei coeficientilor C = [c_i,j]
i,j=1, ... ,p+1 si a vectorului termenilor liberi D =
[d_ j] j=1, ... , p+1:
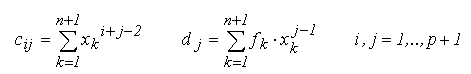
- Rezolvarea sistemului de ecuatii C a = D si determinarea coeficientilor a_j , j=1, ... , p+1.
- Aproximarea functiei in punctul de calcul:
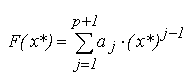
Daca polinomul de aproximare are gradul p=1, aplicarea criteriului celor mai mici patrate conduce la regresia liniara:
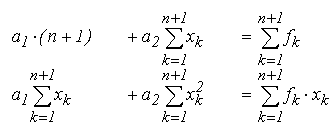
![]() - valoarea medie a variabilei statistice x;
- valoarea medie a variabilei statistice x;
![]() - valoarea medie a variabilei statistice f;
- valoarea medie a variabilei statistice f;
![]() - valoarea medie patratica a variabilei statistice x;
- valoarea medie patratica a variabilei statistice x;
![]() - valoarea medie a variabilei x * f;
- valoarea medie a variabilei x * f;
cov (x,f) - covarianta statistica a variabilelor x si f;
![]() - dispersia variabilei x in raport cu valoarea sa medie,
- dispersia variabilei x in raport cu valoarea sa medie,
unde :
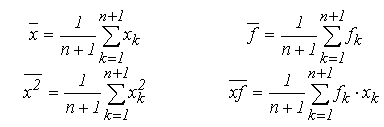
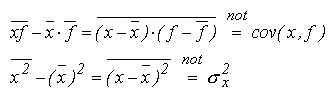
Solutia sistemului de ecuatii este:
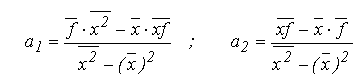
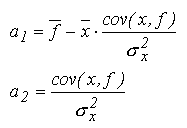
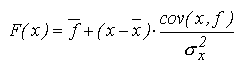
Algoritmul pentru regresia liniara este asemanator si reprezinta un caz particular al algoritmului pentru regresia polinomiala.
Pentru aceasta tema, care este un caz particular al regeresiei polinomiale,
suportul teoretic si algoritmul se pregatesc individual de catre studenti,
dupa modelul regresiei liniare.
Pentru implementarea algoritmelor
corespunzatoare diferitelor forme de regresie
se poate consulta cartea