Lucrarea 4. Tehnici de pivotare, inversare matriceala si rezolvarea sistemelor de ecuatii liniare triunghiulare: substitutia inainte/inapoi
Tema A - Pivotarea
partiala
Tema B - Inversarea
unei matrice prin eliminare Gauss-Jordan
Tema C - Triunghiularizarea
Gauss si substitutia inainte / inapoi
Un sistem de ecuatii liniare are forma generala:
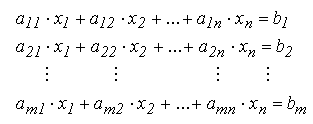
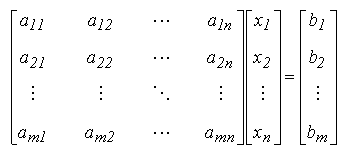
In functie de raportul in care se gasesc numarul de necunoscute n si numarul de ecuatii m se disting:
- sisteme determinate (m=n)
- sisteme nedeterminate (m<> n), care la randul lor pot fi supradeterminate (m>n) sau subdeterminate (m<n).
In continuare se iau in discutie numai sistemele liniare.
Metodele numerice folosite pentru rezolvarea sistemelor de ecuatii liniare
se impart in doua mari categorii: metode directe si metode iterative.
Metodele directe, numite uneori si exacte permit determinarea solutiei
exacte (in ipoteza unei masini ideale) intr-un numar finit de pasi.
Aceste metode apeleaza la transformarea sistemului originar intr-un
sistem echivalent, cu o structura mai simpla, ce poate fi rezolvat pe cai
elementare. Metode directe: Inversarea matricei coeficientilor, Triunghiularizarea
Gauss, Factorizarea Crout sau Doolitle, Factorizarea Cholesky.
Metodele iterative, denumite si metode aproximative, nu pot calcula
solutia exacta - chiar si in ipoteza unei masini ideale - decat intr-un
numar infinit de pasi sau iteratii. Aceste metode pornesc de la o aproximatie
initiala a solutiei exacte si construiesc un sir de aproximatii succesivecare,
in anumite conditii, converge catre solutia exacta. Metode iterative: Metoda
Jacobi, Metoda Seidel-Gauss, Metoda suprarelaxarii succesive, Metoda Southwell,
Metode de gradient.
Metodele directe foloseste o serie de matrice elemenetare de transformare (pe scurt transformari elementare). Aceste matrice se definesc pornind de la matricea unitate de rang egal cu rangul matricei supuse transformarii si au urmatoarele forme:
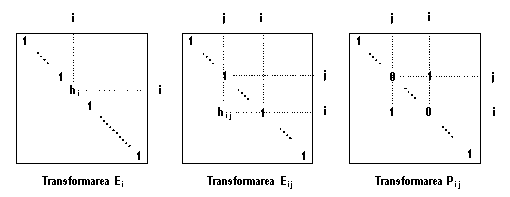
- Matricea E_i, care se obtine din matricea unitate de rang n, a carei linie i a fost inmultita cu scalarul h_i. Premultiplicarea / postmultiplicarea matricei A cu transformarea elementara E_i este echivalenta cu inmultirea liniei / coloanei i a matricei A cu scalarul h_i.
- Matricea E_ij care se obtine din matricea unitate de rang n prin inlocuirea elementului nul de pe linia i si coloana j (i <> j) cu scalarul h_ij. Premultiplicarea / postmultiplicarea matricei A cu transformarea elementara E_ij este echivalenta cu adunarea liniei / coloanei j din matricea A, inmultita cu scalarul h_ij la linia / coloana i din aceeasi matrice.
- Matricea P_ij se obtine din matricea unitate de rang n prin schimbarea intre ele a liniilor i si j. Premultiplicarea / postmultiplicarea matricei A cu transformarea elementara P_ij este echivalenta cu schimbarea intre ele a liniilor / coloanelor i si j din matricea A.
Pentru majoritatea metodelor de rezolvare a sistemelor de ecuatii liniare
- fie ele directe sau iterative - se ajunge ca la un moment dat sa fie
necesara impartirea la un element diagonal din matricea A, notat
generic a_ jj. Acest element poarta numele generic de pivot.
Desigur, daca acest element este nul metoda respectiva esueaza, deoarece - din punct
de vedere numeric - operatia de impartire la 0 este imposibila si, daca
nu se iau masuri speciale, orice program de calcul se intrerupe din executie
in urma producerii unei erori de tipul "Run time error" si un eventual
mesaj de eroare de genul "Floating point overflow".
Pentru amanunte privind pivotarea
completa si o procedura de implementare a acestei tehnici, se poate consulta
cartea
Situatia extrema in care intr-o matrice A poate sa apara un element
diagonal nul este cea in care matricea respectiva este singulara. Pe de
alta parte, pivotul se poate anula fara ca matricea A sa fie singulara.
Mai mult decat atat, pivotul poate fi nenul, dar cu o valoare foarte mica,
astfel incat impartirea la el sa conduca la producerea unor erori de rotunjire,
care prin acumulare pot denatura rezultatul.
Evitarea unor asemenea situatii se poate face prin adoptarea unei masuri
care sa permita aducerea pe diagonala a unui element suficient de mare.
O asemenea tehnica este pivotarea. Pivotarea inseamna schimbarea
intre ele a doua linii (pivotarea partiala) sau a doua linii si/sau
a doua coloane (pivotarea completa) astfel incat noul pivot sa aiba
o valoare absoluta cat mai mare posibil. Cautarea noului pivot se face
pe coloana curenta j* numai pe liniile situate sub linia
j*, inclusiv aceasta (pivotarea partiala) sau pe liniile si
coloanele situate sub linia j* si la dreapta coloanei
j*, inclusiv acestea (pivotarea completa).
In cazul pivotarii partiale, la un pas j*, se spune ca se executa
pivotarea partiala pe coloana j*. In principiu aceasta tehnica cauta
pe coloana j* elementul subdiagonal maxim in valoare absoluta si
schimba linia j* cu linia in care apare acel element. Deoarece schimbarea
a doua linii in matricea A inseamna de fapt schimbarea ordinii a
doua ecuatii din sistem, se impune ca - simultan - sa se realizeze si schimbarea
termenilor liberi corespunzatori din vectorul b.
Algoritmul 1 - Pivotarea partiala pe
coloana j* a matricei A
Tema B - Inversarea unei matrice prin eliminare Gauss-Jordan
Inversarea matricelor corespunde impartirii intre scalari, dar se deosebeste
de aceasta prin faptul ca nu orice matrice admite inversa. Pentru a putea
fi inversata, o matrice trebuie sa fie patrata si sa aiba determinantul
nenul. Daca o matrice patrata admite inversa, despre acea matrice se mai
spune ca este nesingulara.
Pentru un sistem de ecuatii liniare A*x=b, dupa inversarea matricei
A,
solutia sistemului de ecuatii se determina simplu, printr-o inmultire matriceala
:
Principiul metodei eliminarii Gauss - Jordan poate fi descris sumar, dupa cum urmeaza: se considera matricea A de rang n, careia i se aplica o succesiune de p transformari elementare in scopul aducerii matricei A la forma matricei unitate de acelasi rang I_n :
Urmatoarea varianta de aplicare a metodei Gauss - Jordan, desi total neeconomica din punctul de vedere al memoriei ocupate, ilustreaza foarte bine principiul expus mai sus. Matricei de inversat A i se ataseaza in partea dreapta matricea unitate I_n , obtinand matricea extinsa A* = [A | I_n]. Premultiplicarea matricei extinse cu succesiunea de transformari elementare de mai sus conduce la:
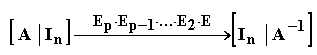
Aplicarea acestor transformari se face respectand urmatoarea schema:
-
fiecare coloana j din
primele n coloane din matricea extinsa A*urmeaza a fi transformata
in coloana a matricei unitate, de forma C_ j= [0...0 1 0...0]t , unde
elementul nenul apare in pozitia j. In acest scop, linia j din
matricea A* se imparte la elementul diagonal a_ j j pentru a
obtine elementul unitar al vectorului C_ j :
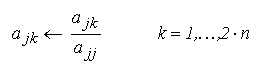
-
In continuare, urmeaza sa se obtina
elementele nule ale vectorului C_ j. In acest scop, pentru fiecare
linie i (i <> j ) din matricea A*, linia j
se inmulteste cu scalarul a_ij si se scade din linia i :
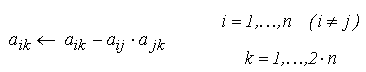
Algoritmul 2 - Eliminarea Gauss-Jordan aplicata matricei extinse A*
- Definirea sistemului de ecuatii : rangul n, matricea coeficientilor A si vectorul termenilor liberi.
- Extinderea matricei A, la dreapta, cu matricea unitate: a_i,j+n = 0 (i, j=1,...,n) si a_i,i+n = 1 (i=1,...,n).
- Calculul inversei :
- Initializarea coloanei curente din matricea A* care se transforma in coloana a matricei unitate : j <-- 1.
- Se executa pivotarea partiala pe coloana j.
- Se obtine elementul diagonal unitate pe coloana j : a_ j,k <-- a_ j,k / a_ j, j (k=1,...,2*n)
- Se obtin elementele nule pe coloana j : a_i,k <-- a_i,k - a_i,j * a_ j,k (i=1,...,n ; i<>j ; k=1,...,2*n)
- Se trece la urmatoarea coloana supusa transformarii : j <-- j+1. Daca j <= n, se revine la pasul 3.ii. Daca j > n se trece la pasul 4.
- Calculul necunoscutelor
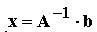 ,
unde
,
unde 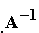 este
formata din ultimele n coloane ale matricei extinse.
este
formata din ultimele n coloane ale matricei extinse.
Pentru o varianta compacta a eliminarii
Gauss-Jordan (se lucreaza pe loc in matricea A), se poate consulta
cartea
"Calcul numeric cu aplicatii in Turbo Pascal".
Tema C - Triunghiularizarea Gauss si substitutia inainte / inapoi
Triunghiularizarea Gauss aduce sistemul initial de ecuatii la o forma superior sau inferior triunghiulara, care se rezolva apoi folosind substitutia inapoi sau inainte. In continuare se descrie numai triunghiularizarea Gauss corespunzatoare formei superior triunghiulare.
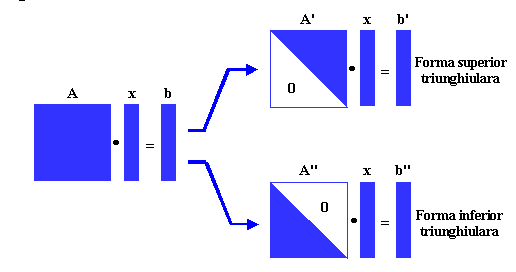
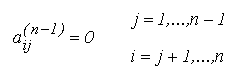
Procedura de triunghiularizare se desfasoara in n-1 pasi, la fiecare pas j anulandu-se elementele subdiagonale de pe coloana j (nu este nevoie si de un ultim pas j=n, deoarece pe ultima coloana a matricei nu exista elemente subdiagonale).
Vom considera un pas generic j si vom nota cu A(j-1), respectiv A(j) formele matricei inainte si dupa efectuarea transformarilor din pasul curent. Pentru anularea unui element a_ij ( j-1 ) situat pe linia i > j matricea A(j-1) se premultiplica cu transformarea elementara E_ij aleasa pentru a raspunde scopului urmarit, si anume anularea elementului a_ij ( j ). Prin urmare, putem scrie:
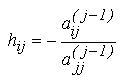
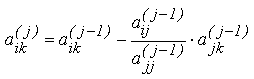
Pentru pastrarea echivalentei intre sistemul initial de ecuatii si cel la care se ajunge prin triunghiularizare, este necesar ca transformarile care se realizeaza in matricea A sa se regaseasca si in structura vectorului termenilor liberi b. In acest scop, la fiecare pas j, transformarea P(j) (pivotarea) si cele n-j transformari de tipul E_ij , se aplica si vectorului termenilor liberi. Astfel, pentru linia i, folosind multiplicatorul h_ij calculat anterior, se recalculeaza si termenii liberi:
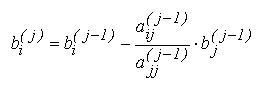
Algoritmul 3 - Triunghiularizarea Gauss compacta (pe loc, in matricea A)
- Definirea sistemului de ecuatii: rangul n, matricea coeficientilor A si vectorul termenilor liberi b.
- Triunghiularizarea sistemului de ecuatii:
- Initializarea coloanei curente din matricea A : j <-- 1;
- Se executa pivotarea partiala permutand numai elementele de pe liniile j si j* aflate la dreapta coloanei j, inclusiv aceasta; j* este indicele liniei pe care a fost localizat noul pivot;
- Eliminarea necunoscutei x_ j din toate ecuatiile subiacente:
- Initializarea liniei curente din care se elimina necunoscuta x_j : i <-- j+1 ;
- Calculul multiplicatorului h_ij memorat in variabila Temp :
Temp <-- - a_ ij / a_ jj - Actualizarea elementelor de pe linia i a matricei A
si vectorului b :
a_ik <-- a_ik + Temp * a_ jk , k = j+1, ... , n b_i <-- b_i + Temp * b_ j - Se trece la urmatoarea linie din care se elimina necunoscuta x_j : i <-- i+1. Daca i <= n se revine la pasul 2.iii.a. Daca i > n se trece la pasul 2.iv.
- Se trece la urmatoarea coloana supusa transformarii : j <-- j+1. Daca j <= n-1 se revine la pasul 2.ii. Daca j > n-1 se trece la pasul 3.
- Partea superioara a matricei A (pe diagonala principala si deasupra acesteia) si vectorul b contin forma triunghiulara a sistemului de ecuatii. Pentru rezolvarea acestuia se aplica substitutia inapoi.
Un sistem de ecuatii liniare de forma triunghiulara se rezolva prin substutie inapoi (sisteme superior triunghiulare) sau substitutie inainte (sisteme inferior triunghiulare). Principiul acestor mecanisme este ilustrat pentru substitutia inapoi si un sistem de 4 ecuatii si 4 necunoscute.
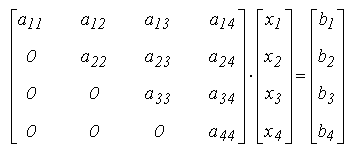
Generalizand, un sistem triunghiular de rang n se rezolva in n pasi succesivi. La fiecare asemenea pas se determina una din necunoscute (din ecuatia care o izoleaza) si se elimina necunoscuta calculata din ecuatiile precedente, obtinandu-se un sistem triunghiular de rang cu o unitate mai mic. Deoarece ordinea de determinare a necunoscutelor este x_n, x_(n-1), ... , x_2, x_1 metoda este numita substitutie inapoi.
Ecuatiile care descriu substitutia inapoi sunt:
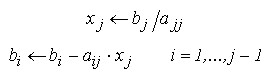
Algoritmul 4 - Rezolvarea sistemelor triunghiulare prin substitutie inapoi
- Definirea sistemului de ecuatii: rangul n, matricea coeficientilor A (superior triunghiulara), vectorul termenilor liberi b.
- Substitutia inapoi:
- Initializarea numarului de ordine al necunoscutei care se determina: j <-- n;
- Determinarea necunoscutei x_ j care se memoreaza in
vectorul termenilor liberi:
b_ j <-- b_ j / a_ jj - Eliminarea necunoscutei x_ j din primele j-1
ecuatii, prin recalcularea termenilor liberi ai acestora:
b_i <-- b-i - a_ ij * b_ j i = 1, ... , j-1 - Se trece la tratarea urmatoarelor necunoscute: j <-- j-1. Daca j >= 1 se revine la pasul 2.ii. Daca j < 1 se trece la pasul 3.
- Vectorul termenilor liberi b contine solutiile sistemului de ecuatii.
Pentru detalii suplimenatre privind
procedura de triunghiularizare Gauss si procedeele de substitutie, se poate
consulta cartea
"Calcul
numeric cu aplicatii in Turbo Pascal".