Lucrarea 7.
Tehnici de lucru cu matrice rare aplicate sistemelor de ecuatii liniare
Exista aplicatii in care intervin matrice de dimensiuni mari care, in plus, se caracterizeaza printr-o forma speciala a acestor matrice, in sensul in care numai un numar redus de elemente au valori semnificative, nenule. Asemenea matrice au capatat denumirea de matrice rare, lacunare sau sparse. Caracterizarea matricelor de acest tip se face cu ajutorul factorului de lacunaritate, definit ca raportul dintre numarul elementelor nenule si numarul total al elementelor matricei. Numeroase probleme practice folosesc matrice rare al caror factor de lacunaritate poate ajunge pana la valori de 0,02 - 0,03. Iata citeva exemple de structuri ale unor matrice rare.
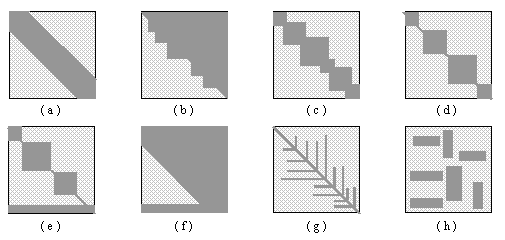
(a) - matricea diagonala banda; (b) matrice bloc - triunghiulara; (c) - matrice bloc tridiagonala; (d) matrice bloc-diagonala; (e) matrice bloc - diagonala marginita; (f) matrice triunghiulara banda marginita; (g) si (h) alte forme speciale de matrice rare
Este evident ca in asemenea situatii memorarea elementelor nule din matrice
nu se justifica sub nici o forma din punctul de vedere al memoriei ocupate.
In plus, operatiile cu asemenea matrice presupun efectuarea a numeroase
adunari / inmultiri cu zero, care nu fac decat sa consume inutil din timpul
de calcul. Plecand de la aceste observatii au fost elaborate tehnici speciale
de lucru cu matrice rare. Aceste tehnici asigura atat micsorarea necesarului
de memorie, cat si reducerea timpului de calcul prin eliminarea operatiilor
aritmetice cu rezultat previzibil.
Index:
Memorarea unei matrice rare se face sub forma unor liste unidimensionale
- deci a unor vectori - care contin numai elementele nenule din matrice.
Eliminarea elementelor nule face imposibila adresarea in continuare a unui
element oarecare in forma traditionala, prin indicarea liniei si coloanei
la intersectia carora se afla acesta - de ex. a(1,5) sau a(4,9).
Pe de alta parte, utilizarea ulterioara in calcule a matricei impune existenta
unei modalitati de adresare a elementelor sale. Prin urmare, lista(ele)
in care se memoreaza matricea A trebuie sa contina sub o forma sau
alta cate trei componente pentru fiecare element nenul al matricei: linia
si coloana unde se afla acel element si valoarea acestuia.
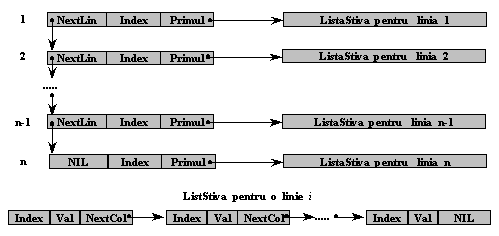
Se folosesc doua liste, cu urmatoarea structura:
Dintre solutiile de memorare (stocare) a matricelor rare existente, vom
descrie memorarea in liste inlantuite. Aceasta tehnica de
memorare apeleaza la notiunea de variabila dinamica sau pointer,
asa cum este cunoscuta in limbajul Pascal. Listele inlantuite memoreaza
pe langa informatiile referitoare strict la matrice (valori si localizari)
si informatii cu privire la localizarea elementelor respective in memoria
dinamica.
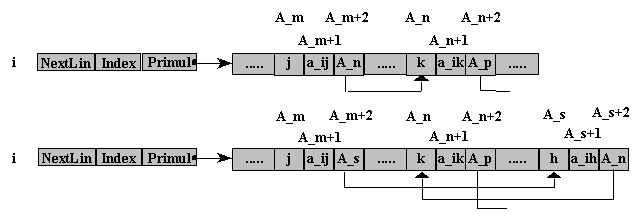
Se doreste adaugarea unui nou element nenul pe linia i, in coloana h, situata intre coloanele j si k. Se creeaza un nou element in ListaStiva la adresa A_s, in care se inscrie valoarea elementului a_ih. Campul NextCol la care este inscris elementul din coloana j se inscrie cu adresa de memorie a elementului nou creat, A_s, iar in campul NextCol al acestuia se inscrie adresa catre care indica anterior campul NextCol al elementului a_ij.
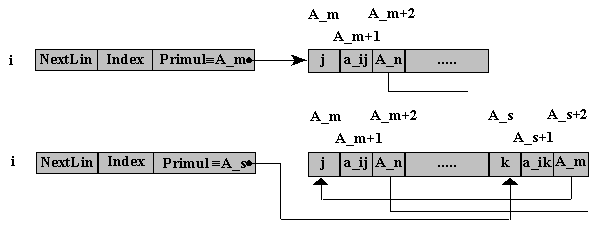
Se doreste adaugarea unui nou element pe linia i, in prima pozitie in ListaStiva, corespunzator unei coloane k, ce precede coloana j a elementului deja existent. Se creeaza un nou element in ListaStiva la adresa A_s, in care se inscrie valoarea elementului a_ik. In campul NextCol al elementului nou creat se copie adresa existenta in campul Primul din ListaLinii, iar in acest camp se inscrie adresa A_s.
Eliminarea unui element din interiorul ListeiStiva
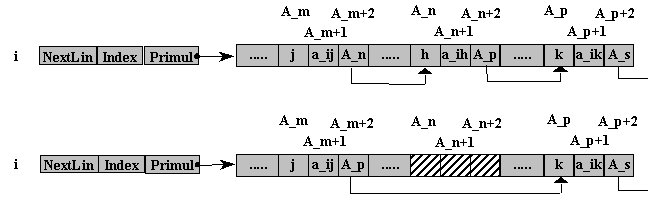
Se doreste eliminarea unui element de pe linia i si coloana h, situata intre coloanele j si k. Se copie adresa catre care indica campul NextCol al elementului ce se elimina in campul omonim al elementului ce-l precede, a_ij, dupa care zona de memorie afectata elementului a_ih este declarata disponibila.
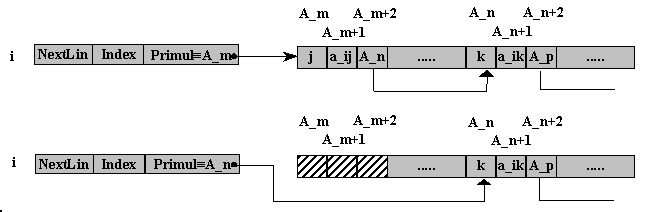
Se doreste eliminarea elementului de pe linia i si coloana j, care se gaseste primul in ListaStiva. Se copie adresa catre care indica campul NextCol al elementului eliminat in campul Primul din ListaLinii, dupa care zona de memorie afectata elementului a_ij este declarata disponibila.
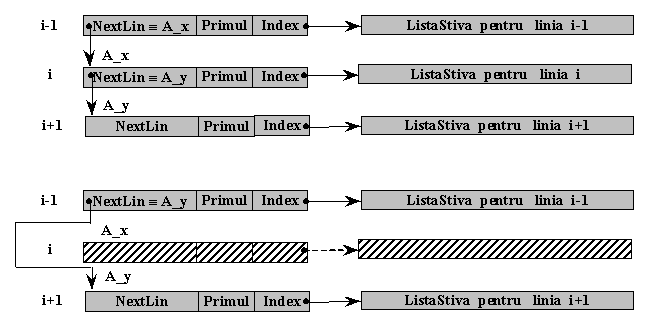
Se doreste eliminarea liniei i. Se copie adresa catre care indica campul NextLin asociat liniei ce se elimina in campul omonim al componentei precedente, dupa care se elibereaza zona de memorie afectata liniei i. Inainte de eliberarea elementului i din ListaLinii se elibereaza ListaStiva asociata liniei respective.
Orice matrice trebuie privita ca o structura dinamica, care se creeaza
atunci cand este necesar si se distruge atunci cand nu mai este nevoie
de ea. Ea poate fi descrisa cu ajutorul unui tip inregistrare (record)
cu patru componente: numele matricei Nume, dimensiunile ei
Lin
si Col si adresa de memorie de la care incepe memorarea elementelor
nenule ale matricei Orig. Deoarece campul Orig
urmeaza sa memoreze o adresa de memorie, tipul asociat lui este pointer.
Astfel, se defineste tipul inregistrare (record) MatriceSp
pentru definirea unei matrice sparse:
type MatriceSp= record
Nume : string;
Lin,Col : integer;
Orig : pointer;
end;
type MatSp =
^MatriceSp;
Cele doua liste in care se memoreaza
propriu-zis elementele nenule din matrice vor avea o structura inlantuita,
conform celei descrise in figura :
type ListaLinii= ^Linie;
Linie = record
NextLin : ListaLinii;
Index : integer;
Primul : pointer;
end;
type ListaStiva=^Coloane;
Coloane = record
Index : integer;
Val : real;
NextCol : ListaStiva;
end;
![]() Inapoi la Index
Inapoi la Index
Exemple pentru lucrul cu matrice rare :
Exemplul 1 :
Crearea unei variabile dinamice pentru memorarea unei matrice rare
Exemplul 2 :
Conversia unei matrice complete in matrice rara
Exemplul 3 :
Pozitionarea pe o linie a matrieci rare
Exemplul 4 :
Pozitionarea pe o coloana a matrieci rare
Exemplul 5 :
Adaugarea unui element nenul intr-o matrice rara
Studentii vor elabora procedurile pentru urmatoarele tipuri de prelucrari :
- Eliminarea unui element nenul dintr-o matrice rara.
- Eliminarea unei linii dintr-o matrice rara.
- Eliminarea unei coloane dintr-o matrice rara.
- Adunarea a doua matrice rare.
Exemplul
1 : Crearea unei variabile dinamice pentru memorarea unei matrice rare
procedure CreareMatSp (
var
x : MatSp ; Nume :string
;L,C : integer);
{Procedura CreareMatSp creeaza
o variabila dinamica de tip MatriceSp in structura careia
urmeaza sa fie memorata matricea rara. Matricea x va avea
dimensiunile [1..L,1..C] si i se va asocia numele Nume.}
var z, Tempz:ListaLinii
;
begin
i : integer ;
new (x)
; {Se creeaza o variabila dinamica de tipMatriceSp}
end ;
x^.Nume:=Nume;
x^.Lin := L;
x^.Col := C;
new (z);
{Se creeaza prima linie}
x^.Orig := z ;
for i := 1 to L-1
do
begin
new (Tempz) ;
{Se creeaza linia i+1}
end;
z^.NextLin := Tempz ;
z^.Primul := nil ;
{Linie vida}
z^.Index := i ; {Indexul
liniei}
z := Tempz ; {Avansul
in lista existenta}
z^.Primul:= nil ;
{Linie
vida}
z^.NextLin := nil ; {Capatul
listei linii}
z^.Index := L
; {Indexul
ultimei linii}
Exemplul 2 : Conversia unei matrice complete in matrice rara
procedure SparsConvert2 ( a : MatriceR; n : integer; Nume : string; var x : MatSp);
{Procedura SparsConvert2 converteste matricea patrata a [1..n,1..n] din forma completa in forma de memorare cu liste inlantuite. Matricea este memorata in doua liste inlantuite, a caror adresa de origine in memorie se gaseste in campul Orig al variabilei x.}
var i, j, p : integer;
z, Tempz : ListaLinii;
y, Tempy : ListaStiva;
begin
{Creeaza variabila dinamica asociata}end;
CreareMatSp ( x, Nume, n, n);
z:=x^.Orig; {Fixarea pe adresa de start}
for i:=1 to n do
beginp:=1;end;
{Fixarea pe primul element de pe linia i}
y:=z^.Primul;
for j:=1 to n doif (a[i,j]<>0) then{Fixarea pe urmatoarea linie}
begin{Element nou pe linia i } new(Tempy);end;
if p = 1 then
begin {Primul element}p:=0;end
z^.Primul:=Tempy;
else {Element intermediar}y^.NextCol:=Tempy;y:=Tempy;
{Completare a[i,j]}
y^.Index:=j;
y^.Val:=a[i,j];
y^.NextCol:=nil;
z:=z^.NextLin;
Exemplul 3 : Pozitionarea pe o linie a matricei rare
procedure CautaLinSp ( x : MatSp; i : integer; var Ln,Pred : ListaLinii );
{Procedura CautaLinSp parcurge lista ListaLinii asociata unei matrice memorate in listele inlantuite catre care indica pointerul x, pentru a se pozitiona pe componenta corespunzatoare liniei i. Matricea este memorata de la adresa catre care indica x^.Orig. Adresa componentei corespunzatoare liniei i este returnata in pointerul Ln, iar pointerul Pred contine adresa liniei i-1.}
var k : integer ;
begin
Pred:=nil;end;
Ln:=x^.Orig; {Fixarea pe prima linie}
k:=1;
while ( k<i ) do
beginPred:=Ln; {Linia predecesor}end;
Ln:=Ln^.NextLin; {Avans in lista linii}
k:=k+1;
Exemplul 4 : Pozitionarea pe o coloana a matricei rare
procedure CautaColSp ( var y : ListaStiva; j : integer; var ValEx : real; var Pred : ListaStiva);
{Procedura CautaColSp parcurge lista ListaStiva (catre care indica pointerul y ) asociata unei linii dintr-o matrice rara, in cautarea unui element nenul pe coloana j . Procedura returneaza doi parametri: ValEx care indica existenta (<>0) sau absenta (=0) unui element nenul pe coloana j. In primul caz, valoarea parametrului ValEx corespunde valorii elementului nenul. Procedura returneaza in pointerul y adresa componentei cautate, iar in Pred adresa componentei care o precede pe cea cautata.}
begin
Pred:=nil;end;
ValEx:=0;
while (y<>nil) and (y^.Index<>j) do
beginPred:=y;end;
y:=y^.NextCol;
if (y<>nil) and (y^.Index=j) then ValEx:=y^.Val;
Exemplul 5 : Adaugarea unui element nenul intr-o matrice rara
procedure AdaugaElemSp ( x : MatSp; i , j : integer; v : real);
{Procedura AdaugaElemSp insereaza un element nenul pe linia i si coloana j a matricei rare memorate in listele inlantuite catre care indica x^.Orig.}
var z, z1 : ListaLinii;
y,
Pred, Tempy : ListaStiva;
ValEx
: real;
begin
{Test pentru conformitatea dimensiunilor}end;
if ( i > x^.Lin ) or ( j > x^.Col )
then MesajEroare('AdaugaElemSp','Dimensiuni neconforme !!!')
else
beginCautaLinSp( x, i, z, z1); {Pozitionarea pe linia i }end;
y:=z^.Primul;
if ( y <> nil )
then
beginCautaColSp ( y, j, ValEx, Pred );end
if ( ValEx<>0 )
then y^.Val:=v {Schimba valoare element existent}
else
begin {Se creeaza un nou element}new ( Tempy );end;
if ( y = nil )
then
begin {Inserare la sfarsitul listei}
Tempy^.NextCol:=nil;
Pred^.NextCol:=Tempy;
end
else if ( Pred = nil )
then
begin {Inserare la inceputul listei}
Tempy^.NextCol:=z^.Primul;
z^.Primul:=Tempy;
end
else
begin {Inserare in interiorul listei}
Tempy^.NextCol:=
Pred^.NextCol;
Pred^.NextCol:=Tempy;
end;
Tempy^.Index:=j;
Tempy^.Val:=v;
else
begin {Inserare la inceputul listei vide}
new(Tempy);
Tempy^.NextCol:=nil;
Tempy^.Index:=j;
Tempy^.Val:=v;
z^.Primul:=Tempy;
end;
Pentru detalii suplimenatare privind
procedurile pentru lucrul cu matrice rare, se poate consulta cartea
"Calcul numeric cu aplicatii in Turbo Pascal".