Lucrarea 8. Ecuatii neliniare: metode de partitionare si metode de aproximatii succesive
Index:
Tema A - Metode de partitionare
A.1. Metoda bisectiei
<----------- algoritm
A.2. Metoda secantei
<----------- algoritm
Tema B - Metode de aproximatii
succesive
B.1. Metoda contractiei
<----------- algoritm
B.2. Metoda Newton
<----------- algoritm
Orice ecuatie care nu are forma a * x+b=0 se numeste neliniara si se exprima sintetic:
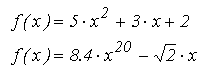
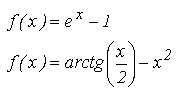
Un punct
Metodele de rezolvare a ecuatiilor neliniare au toate caracter iterativ si se impart in doua mari categorii: metode de partitionare si metode de aproximatii succesive.
Pentru metodele de partitionare, folosind principiul partitionarii, intervalul de lucru este micsorat progresiv, pana la o deschidere suficient de mica pentru a satisface precizia impusa. Metodele din aceasta categorie (metoda bisectiei sau metoda secantei) sunt metode sigure - in sensul in care radacina este intotdeauna izolata intr-un interval suficient de ingust - dar se caracterizeaza printr-o convergenta lenta.
Metodele de aproximatii succesive pornesc de la o aproximatie initiala, pe care o imbunatatesc in pasi succesivi si, in anumite conditii, converg catre solutia exacta. Metoda contractiei si metoda Newton sunt principalele metode de acest tip, dar exista o gama larga de variante ale lor, concepute in scopul imbunatatirii performantelor. Metodele de aproximatii succesive sunt, de regula, mai rapide decat metodele de partitionare, dar prezinta riscul divergentei atunci cand in vecinatatea zeroului cautat, functia f(x) are o comportate specifica.
Tema A - Metode de partitionare
Dupa incadrarea unei solutii exacte, se pot aplica o serie de metode iterative care permit determinarea unei solutii aproximative in limita preciziei impuse. Dintre acestea, metodele de partitionare actioneaza direct asupra intervalului in care a fost incadrata solutia, urmarind "comprimarea" acestuia pana la limita impusa de criteriul de oprire. Din aceasta categorie fac parte metoda bisectiei, metoda secantei si metoda cautarii cu pas variabil. Deoarece la fiecare iteratie, intervalul de lucru incadreaza permanent solutia exacta, convergenta acestor metode este garantata. Din pacate, ele se caracterizeaza printr-un numar mare de iteratii necesare atingerii preciziei impuse, deci prin timpi de calcul mari.
Metoda bisectiei, numita uneori si metoda dihotomiei sau
a injumatatirii intervalelor, este cea mai simpla dintre
metodele de rezolvare a ecuatiilor algebrice si transcendente. Se considera
ca, printr-un procedeu oarecare, s-a reusit localizarea radacinii exacte ![]() a ecuatiei f(x)=0 in intervalul [
a ecuatiei f(x)=0 in intervalul [![]() ,
,![]() ].
In ipoteza in care functia f(x) este continua, iar radacina
].
In ipoteza in care functia f(x) este continua, iar radacina ![]() este singurul zerou al lui f(x) in [
este singurul zerou al lui f(x) in [![]() ,
,![]() ],
la extremitatile intervalului functia ia valori de semne contrare: f(
],
la extremitatile intervalului functia ia valori de semne contrare: f(![]() )
* f(
)
* f(![]() )<0.
)<0.
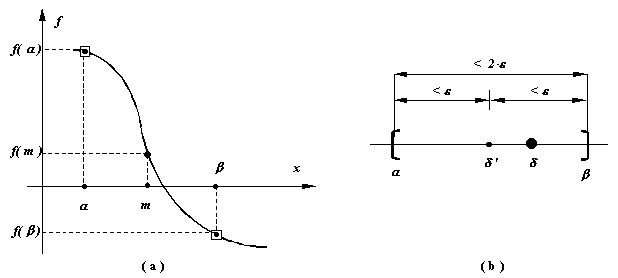
Algoritmul 1 - Ecuatii neliniare - Metoda bisectiei
- Definirea functiei f(x), a intervalului de lucru
[
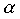 ,
,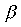 ],
a preciziei
],
a preciziei 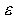 si
a numarului maxim de iteratii Nmax.
si
a numarului maxim de iteratii Nmax. - Procesul iterativ:
- Initializarea procesului iterativ: It <-- 0;
- Daca s-a atins precizia doritta (
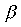 -
-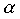 < 2*
< 2*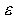 )
sau numarul maxim de iteratii Nmax se incheie bucla iterativa si se trece
la pasul 3.
)
sau numarul maxim de iteratii Nmax se incheie bucla iterativa si se trece
la pasul 3. - Se trece la o noua iteratie: It <-- It+1;
- Injumatatirea intervalului curent:
m <-- (
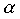 +
+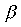 )/2
;
)/2
; - Stabilirea noului interval de lucru:
- Daca f(m) * f(
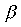 )<0,
radacina se gaseste in [m ,
)<0,
radacina se gaseste in [m , 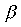 ];
se actualizeaza limita stanga:
];
se actualizeaza limita stanga: 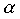 <--
m si se trece la pasul 2.vi;
<--
m si se trece la pasul 2.vi; - Daca f(m) * f(
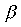 )>0,
radacina se gaseste in [
)>0,
radacina se gaseste in [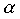 , m];
se actualizeaza limita dreapta:
, m];
se actualizeaza limita dreapta: 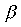 <--
m si se trece la pasul 2.vi;
<--
m si se trece la pasul 2.vi; - Daca f(m) * f(
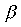 )=0,
radacina este m; se actualizeaza ambele limite:
)=0,
radacina este m; se actualizeaza ambele limite: 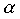 <--
m,
<--
m,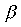 <-- m
si se trece la pasul 2.vi;
<-- m
si se trece la pasul 2.vi;
- Daca f(m) * f(
- Se revine la pasul 2.ii;
- Calculul radacinii aproximative:
x <-- (
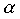 +
+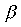 )/2.
)/2.
Metoda secantei, numita si metoda partilor proportionale,
restrange intervalul [![]() ,
,![]() ]
ce incadreaza solutia exacta in iteratia curenta prin raportarea la valorile
functiei la extremitatile intervalului. Astfel, daca noua aproximatie x
se alege astfel incat solutia exacta sa se gaseasca in intervalul [
]
ce incadreaza solutia exacta in iteratia curenta prin raportarea la valorile
functiei la extremitatile intervalului. Astfel, daca noua aproximatie x
se alege astfel incat solutia exacta sa se gaseasca in intervalul [![]() ,
x], valoarea lui x rezulta din egalitatea proportiilor:
,
x], valoarea lui x rezulta din egalitatea proportiilor:
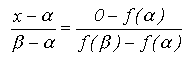
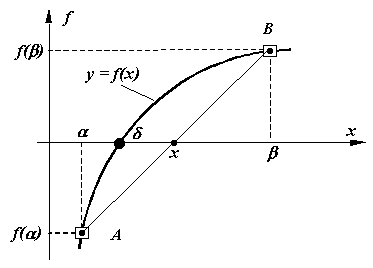 Interpretarea geometrica a acestei relatii corespunde constructiei din
figura. Astfel, pe intervalul [
Interpretarea geometrica a acestei relatii corespunde constructiei din
figura. Astfel, pe intervalul [![]() ,
,![]() ]
curba y=f(x) este aproximata prin dreapta ce trece prin cele doua puncte
A
si B de la extremitatile intervalului. In aceste
conditii, solutia exacta (
]
curba y=f(x) este aproximata prin dreapta ce trece prin cele doua puncte
A
si B de la extremitatile intervalului. In aceste
conditii, solutia exacta (![]() ) urmeaza
a fi aproximata prin abscisa punctului de intersectie a dreptei AB
cu axa OX, notata cu x. Noua aproximatie x
se determina impunand conditia ca in ecuatia dreptei AB :
) urmeaza
a fi aproximata prin abscisa punctului de intersectie a dreptei AB
cu axa OX, notata cu x. Noua aproximatie x
se determina impunand conditia ca in ecuatia dreptei AB :
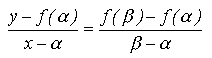
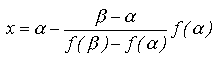
Algoritmul 2 - Ecuatii neliniare - Metoda secantei
- Definirea functiei f(x),
a intervalului de lucru [
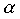 ,
,
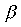 ],
a preciziei
],
a preciziei 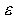 si
a numarului maxim de iteratii Nmax.
si
a numarului maxim de iteratii Nmax. - Procesul iterativ:
- Initializarea procesului iterativ: It <-- 0;
- Daca s-a atins precizia dorita (
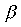 -
-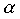 < 2*
< 2*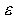 ) sau
numarul maxim de iteratii Nmax se incheie bucla iterativa si se trece
la pasul 3.
) sau
numarul maxim de iteratii Nmax se incheie bucla iterativa si se trece
la pasul 3. - Se trece la o noua iteratie: It <-- It+1;
- Calculul noii aproximatii:
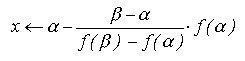
- Stabilirea noului interval de lucru:
- Daca f(m) * f(
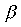 )<0,
radacina se gaseste in [ x,
)<0,
radacina se gaseste in [ x,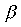 ];
se actualizeaza limita stanga:
];
se actualizeaza limita stanga: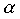 <--
x si se revine la pasul 2.ii.
<--
x si se revine la pasul 2.ii. - Daca f(m) * f(
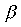 )>0,
radacina se gaseste in [
)>0,
radacina se gaseste in [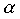 ,x];
se actualizeaza limita dreapta:
,x];
se actualizeaza limita dreapta: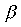 <--
x si se revine la pasul 2.ii.
<--
x si se revine la pasul 2.ii. - Daca f(m) * f(
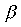 )=0,
radacina este x; se actualizeaza ambele limite:
)=0,
radacina este x; se actualizeaza ambele limite:
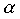 <-- x,
<-- x,
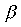 <-- x
si se revine la pasul 2.ii.
<-- x
si se revine la pasul 2.ii.
- Daca f(m) * f(
- Calculul radacinii aproximative: x <--
(
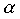 +
+
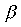 )/2.
)/2.
Tema B - Metode de aproximatii succesive
Dupa cum reiese si din numele lor, metodele de aproximatii succesive
determina o solutie aproximativa a unei ecuatii neliniare prin construirea
unui sir de aproximatii succesive care, in anumite conditii, converge catre
solutia exacta. De aceasta data nu se mai actioneaza asupra intervalului
in care a fost izolata solutia exacta. Acest interval este folosit numai
pentru stabilirea aproximatiei initiale, care poate fi aleasa, in
principiu, oriunde in interiorul acestuia. Din categoria metodelor de aproximatii
succesive fac parte metoda contractiei
si metoda Newton.
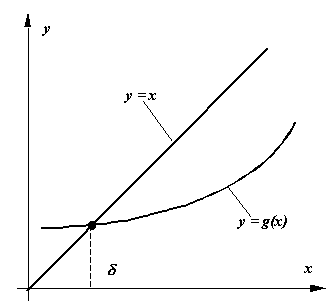 O caracteristica a metodelor de aproximatii succesive se refera la
interpretarea geo- metrica ce se asociaza procesului iterativ. Pentru
metodele de partitionare, rezolvarea ecuatiei f(x)=0 se face prin
determinarea din aproape in aproape, pana la o precizie impusa, a punc- tului
de intersectie a curbei y=f(x) cu axa absciselor. Metodele de aproximatii
succesive inlocuiesc ecuatia sub forma implicita f(x)=0 cu o ecuatie
echivalenta exprimata insa explicit:
O caracteristica a metodelor de aproximatii succesive se refera la
interpretarea geo- metrica ce se asociaza procesului iterativ. Pentru
metodele de partitionare, rezolvarea ecuatiei f(x)=0 se face prin
determinarea din aproape in aproape, pana la o precizie impusa, a punc- tului
de intersectie a curbei y=f(x) cu axa absciselor. Metodele de aproximatii
succesive inlocuiesc ecuatia sub forma implicita f(x)=0 cu o ecuatie
echivalenta exprimata insa explicit:
Inlocuirea ecuatiei f(x)=0 printr-o ecuatie explicita x=g(x) se poate realiza, de regula, pe mai multe cai. Cea mai simpla dintre acestea determina functia g(x) sub forma:
Convergenta procesului iterativ este guvernata de o teorema de punct fix care, in principiu, impune urmatoarele conditii: pentru un interval [
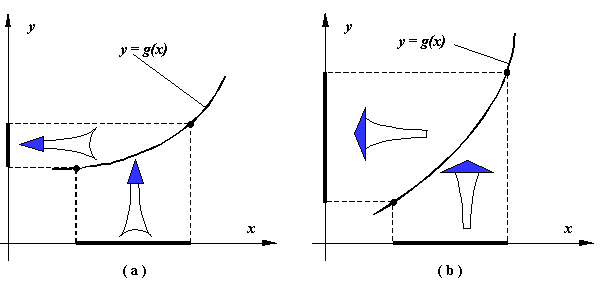
Evolutia unor procese iterative convergente sau divergente este ilustrata in figura de mai jos. In functie de semnul derivatei g' in vecinatatea solutieiInterpretarea geometrica a notiunii de "aplicatie strict contractanta". (a) Functia g(x) este o aplicatie strict contractanta pe un anumit interval daca proiectia acestui interval pe axa Oy, prin curba y = g(x) se contracta. (b) In caz contrar, cand proiectia intervalului respectiv pe axa Oy, prin curba y = g(x) se dilata, g(x) nu mai este o aplicatie strict contractanta.
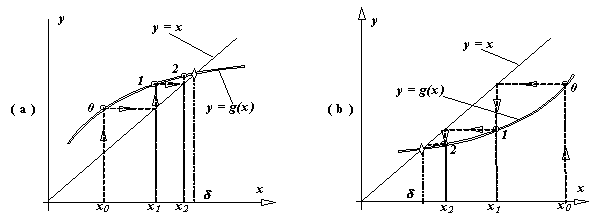
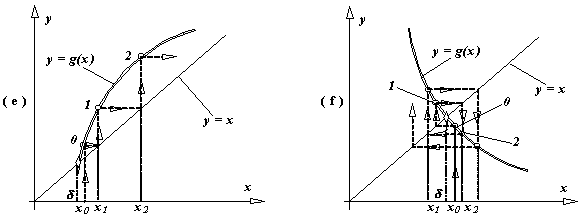
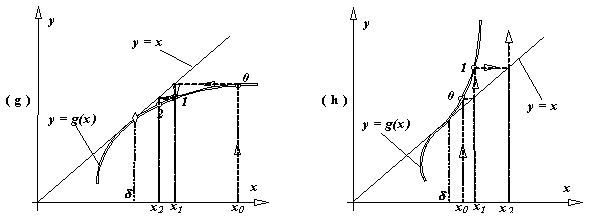
Verificarea conditiilor teoremei de punct fix este insa o sarcina mult
prea neproductiva din punctul de vedere al timpului de calcul si al complexitatii
calculelor pentru a fi si practica. Se prefera verificarea, cel mult, a
unei conditii de forma |g'(![]() )|
< 1 si localizarea stricta a solutiei
)|
< 1 si localizarea stricta a solutiei ![]() ,
iar cel mai frecvent se impune un numar maxim de iteratii la epuizarea
carora procesul iterativ este intrerupt fortat.
,
iar cel mai frecvent se impune un numar maxim de iteratii la epuizarea
carora procesul iterativ este intrerupt fortat.
Algoritmul 3 - Ecuatii neliniare - Metoda contractiei
- Definirea functiei f(x), a aproximatiei initiale x, a preciziei Eps si a numarului maxim de iteratii Nmax.
- Construirea functiei g(x) = x + f(x).
- Procesul iterativ:
- Initializarea procesului iterativ: It <-- 0;
- Daca s-a atins precizia dorita (|f(x)|<Eps) sau numarul maxim de iteratii (It=Nmax) se intrerupe bucla iterativa si se trece la pasul 4.
- Se trece la o noua iteratie: It <-- It+1;
- Calculul noii aproximatii: x <-- g(x)
- Se revine la pasul 3.2.
- Stabilirea conditiilor de iesire din bucla iterativa:
- Daca |f(x)|<Eps - proces convergent - solutia aproximativa este x.
- Daca |f(x)|>=Eps si It=Nmax, se afiseaza mesajul "Depasire numar maxim iteratii".
Una dintre cele mai cunoscute si mai folosite tehnici de rezolvare a ecuatiilor neliniare este metoda Newton, denumita uneori si metoda Newton-Raphson sau metoda tangentelor. Ea se deosebeste de alte metode de aproximatii succesive prin faptul ca pentru fiecare punct din sirul aproximatiilor este necesara atat evaluarea functiei f(x) ce defineste ecuatia, cat si a derivatei acesteia f '(x).
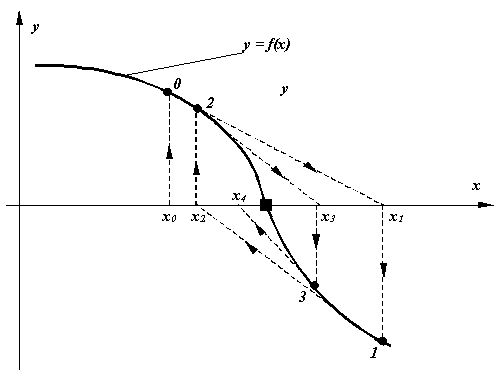
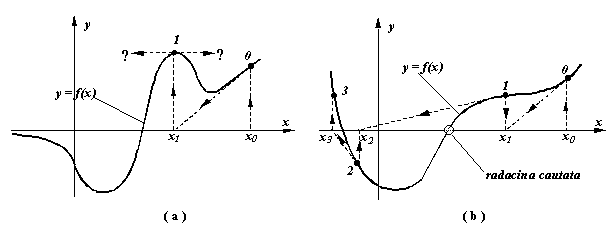
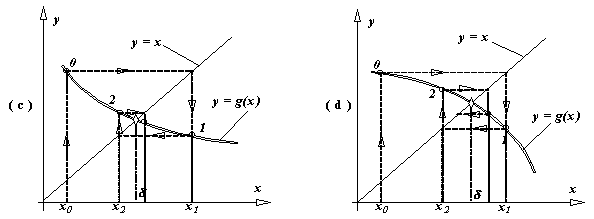
Din punct de vedere formal, metoda Newton foloseste formula de recurenta (iterare):Alegerea aproximatiei initiale influenteaza in buna masura procesul iterativ. (a) Daca aproximatia initiala este prea departe de solutia exacta, este posibil ca, datorita unei forme aparte a curbei y = f(x), noile aproximatii sa fie aruncate spre infinit. (b) Intr-o situatie mai fericita, procesul ramane convergent, dar sirul aproximatiilor succesive se indreapta catre o alta radacina decat cea cautata.
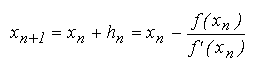
Marele avantaj al metodei Newton este rata mare de convergenta. In apropierea solutiei exacte, se asigura practic dublarea numarului de cifre exacte ale solutiei calculate la fiecare iteratie. Aceasta proprietate remarcabila este "cartea de vizita" ce recomanda metoda Newton ca fiind cea mai eficienta cale de rezolvare a unei ecuatii neliniare pentru care este posibila evaluarea derivatei f '(x). Remarcati totusi precizarea din fraza anterioara ("In apropierea solutiei exacte...") si nu uitati conditiile de convergenta atat de alambicate, care se refera atat la functia f(x), cat si la primele sale doua derivate. Din aceste cauze, despre metoda Newton se spune ca are proprietati locale de convergenta foarte bune, dar se poate comporta lamentabil la nivel global. In situatiile din urma metoda Newton poate fi aplicata ca o procedura terminala, pentru rafinarea eficienta si foarte rapida a unei aproximatii obtinute prin aplicarea, in prima faza, a unei alte metode, mai putin sensibile din punctul de vedere al convergentei dar, in principiu, mai lenta.
Algoritmul 4 - Ecuatii neliniare - Metoda Newton
- Definirea functiei f(x), a derivatei f '(x), a aproximatiei initiale x, a preciziei Eps si a numarului maxim de iteratii Nmax.
- Initializarea procesului iterativ: It <-- 0;
- Procesul iterativ:
- Se trece la o noua iteratie: It <-- It+1;
- Calculul corectiei: dx <-- - f(x) / f '(x)
- Calculul noii aproximatii: x <-- x + dx
- Daca s-a atins precizia dorita (|dx| <= Eps) sau numarul maxim de iteratii (It=Nmax) se intrerupe bucla iterativa si se trece la pasul 4.
- Se revine la pasul 3.1.
- Stabilirea conditiilor de iesire din bucla iterativa:
- Daca |dx|<Eps - proces convergent - solutia aproximativa este x.
- Daca |dx|>=Eps si It=Nmax, se afiseaza mesajul "Depasire numar maxim iteratii".
Pentru detalii suplimenatare privind
metodele de rezolvare a ecuatiilor neliniare, se poate consulta cartea
"Calcul numeric cu aplicatii in Turbo Pascal".