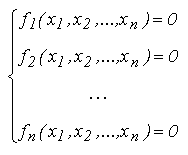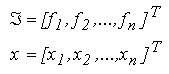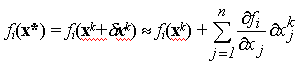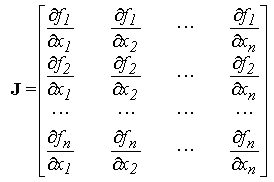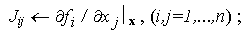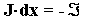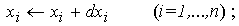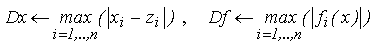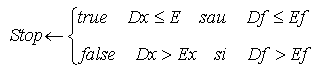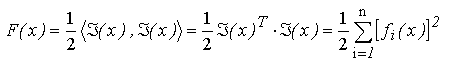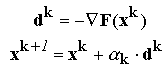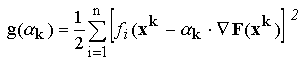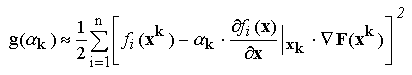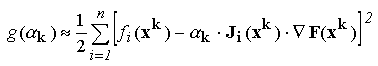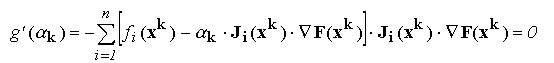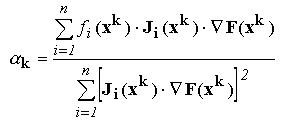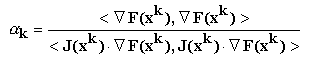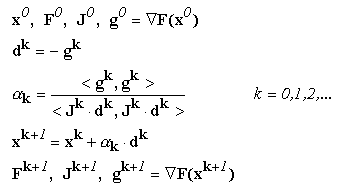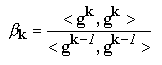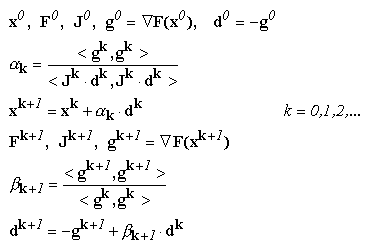Metode
numerice - Aplicatii
Lucrarea 10.
Rezolvarea sistemelor de ecuatii neliniare: metoda Newton si metode de
gradient
Tema A - Metoda Newton
<----------- algoritm
Tema B - Metode de descrestere
Modelul general
al unui sistem de ecuatii neliniare de ordin n are forma:
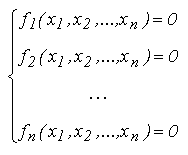
unde
f1, f2, ... , fn
sunt functii neliniare ce depind de variabilele
x1, x2, ... , xn
care, la randul lor, reprezinta necunoscutele problemei. Cele
n
functii si
n variabile pot fi privite ca doi vectori:
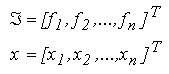
astfel incat sistemul poate fi
scris compact, sub forma:
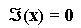
Se considera ca sistemul
de ecuatii neliniare admite solutia exacta
x* = [x*1, x*2, ... , x*n]T,
iar in vecinatatea lui
x*, toate functiile
fi si derivatele
lor partiale
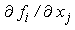
sunt
continue. Toate metodele practice de rezolvare a sistemului
de ecuatii neliniare sunt metode de tip iterativ. Exista si o serie de
metode directe, dar acestea sunt mult prea specifice, referindu-se la forme
cu totul si cu totul particulare ale sistemului. In principiu, exista trei
mari categorii de metode iterative de rezolvare a sistemelor de ecuatii
neliniare:
-
metode bazate pe exprimarea explicita
echivalenta a ecuatiilor sistemului, denumite pe scurt, chiar daca impropriu,
metode de aproximatii succesive;
-
metode care folosesc derivatele
partiale ale functiilor fi, denumite metode de tip Newton;
-
metode de minimizare, numite si
metode de descrestere sau metode de gradient;
Primele doua categorii
de metode sunt principial asemanatoare cu metodele omonime destinate
rezolvarii ecuatiilor neliniare. O asemenea
constatare nu trebuie sa surprinda, deoarece o ecuatie este un caz particular
al unui sistem de ecuatii.
Tema A - Metoda Newton
Pentru sistemul de ecuatii neliniare :
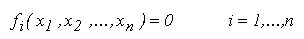
metoda Newton apeleaza la o serie de aproximari care conduc la liniarizarea problemei.
In cele din urma, problema se reduce la rezolvarea unui sir de sisteme de ecuatii
liniare, pentru care se poate aplica oricare din metodele cunoscute.
Admitem ca la iteratia
k s-a determinat o aproximatie
xk = [
x1k, x2k,
... , xnk]
T, care se abate de la solutia
exacta
x* cu vectorul
dxk =
[
dx1k, dx2k, ... , dxnk]
T :
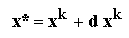
In ipoteza in care abaterile
dxik (
i=1,...,n) sunt
suficient de mici, functiile
fi(
x*) pot fi dezvoltate in serii
Taylor in jurul punctului
xk, retinand numai termenii de
ordinul intai:
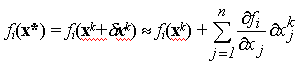
Aceasta expresie poate fi scrisa compact, sub forma matriceala:
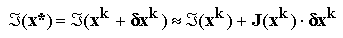
unde matricea
J, formata din derivatele partiale ale functiilor ce definesc sistemul neliniar, este matricea Jacobian:
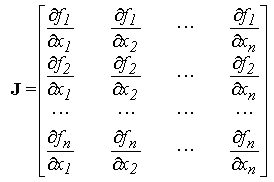
Deoarece
x* reprezinta solutia exacta a problemei,
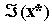
se anuleaza, astfel incat:
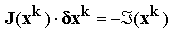
care reprezinta un sistem de ecuatii liniare ce are ca necunoscute corectiile
dxk = [
dx1k, dx2k, ... , dxnk]
T.
Dupa rezolvarea acestui sistem si inlocuirea lui
dxk
se poate determina solutia
x*. Datorita insa neglijarilor
facute la dezvoltarea in serii Taylor, corectiile calculate
dxk
nu mai asigura deplasarea completa din aproximatia
xk
pana la solutia exacta
x*, ci pana la o noua aproximatie a acesteia:
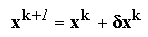
Ultimele doua expresii reprezinta relatiile de recurenta pe baza carora se desfasoara procesul iterativ al metodei Newton, pornind de la o aproximatie
x0.
Conditiile de convergenta ale metodei Newton au o formulare relativ complexa,
iar in practica verificarea lor este, daca nu imposibila, atunci extrem
de costisitoare ca timp de calcul. De aceea, controlul convergentei / divergentei
se face ca si in cazul celorlalte metode iterative, prin impunerea unui numar maxim de iteratii.
Algoritmul 1 - Rezolvarea sistemelor de ecuatii
neliniare cu metotda Newton
-
Definirea sistemului de ecuatii neliniare: ordinul n , functiile
fi(x) si derivatele partiale (i=1,...,n);
-
Definirea parametrilor de iterare: abaterea maxima admisa a aproximatiilor in
doua iteratii succesive Ex, abaterea maxima admisa a functiilor
fi fata de zero Ef si numarul maxim de iteratii Nmax;
-
Definirea aproximatiei initiale xi (i=1,...,n) si calculul
valorilor functiei fi(x) (i=1,...,n);
-
Procesul iterativ:
-
Initializarea procesului iterativ: It <-- 0;
-
Initializarea criteriului de oprire: Stop <-- false;
-
Daca s-a atins numarul maxim de iteratii (It=Nmax) sau s-a atins
criteriul de oprire (Stop=true), se intrerupe procesul iterativ si
se trece la pasul 5;
-
Trecerea la o noua iteratie: It <-- It+1;
-
Memorarea aproximatiei din iteratia anterioara: zi <-- xi
(i=1,...,n);
-
Calculul matricei Jacobian J pentru aproximatia curenta:
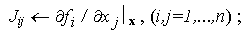
-
Rezolvarea sistemului de ecuatii liniare:
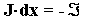
-
Calculul noii aproximatii:
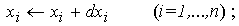
-
Calculul valorilor functiilor pentru noua aproximatie: fi(x)
(i=1,...,n);
-
Calculul abaterilor:
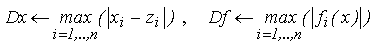
-
Stabilirea valorii criteriului de oprire:
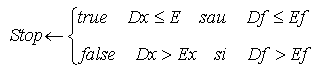
- Se revine la pasul 4.3;
-
Stabilirea conditiilor de iesire din bucla iterativa:
-
daca Stop=true, se afiseaza solutia aproximativa xi (i=1,...,n);
-
daca Stop= false, se afiseaza mesajul "Depasire numar maxim iteratii".
Tema B - Metode de descrestere
Metodele de descrestere reprezinta cai indirecte de rezolvare
a sistemelor de ecuatii neliniare, care transforma sistemul :
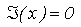
intr-o problema de optimizare neliniara fara restrictii. Sistemului de ecuatii i
se asociaza o functie definita in raport cu toate cele
n necunoscute
F(x) =
F(x1, x2, ... , xn),
care se bucura de proprietatea de a prezenta un punct de extrem (cel mai frecvent
un minim) in solutia exacta a sistemului de ecuatii
x*=[x*1, x*2, ... , x*n]T.
Astfel, prin aplicarea unei metode de optimizare functiei
F(x), in sensul
extremizarii valorii sale, se determina simultan si solutia aproximativa a
sistemului originar. O asemenea functie
F(x) se defineste ca produsul
scalar al functiei asociate sistemului originar cu ea insasi :
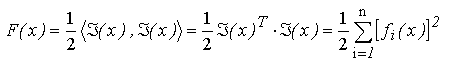
Se verifica simplu ca solutia sistemului de ecuatii reprezinta punctul de minim
global al functiei
F(x).
Dintre metodele de descrestere folosite mai frecvent se
remarca
metoda gradientului si
metoda gradientului conjugat.
Ambele metode minimizeaza functia
F(x) prin deplasarea de la o
aproximatie la alta in lungul unei directii care depinde de gradientul
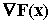
. O
caracteristica remarcabila a acestor metode o reprezinta forma particulara a
expresiei gradientului functiei
F(x):
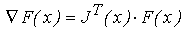
unde
J(x) este matricea Jacobian atasata sistemului originar.
Metoda gradientului
Metoda gradientului porneste de la o aproximatie initiala
x0 pe care cauta sa o imbunatateasca prin aplicarea unor corectii
succesive orientate dupa directia gradientului functiei de optimizat si
proportionale cu acesta. Deoarece vectorul gradient
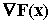
este orientat
intotdeauna in sensul cresterii valorii functiei
F(x), pentru minimizarea
acestei functii corectiile se vor aplica intotdeauna in sens opus gradientului:
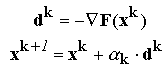
In relatia de mai sus
dk reprezinta directia de deplasare la
iteratia
k, iar
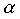 k
k
este un coeficient care descrie amploarea deplasarii in directia
dk.
Coeficientul
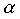 k
k
se alege la fiecare iteratie astfel incat deplasarea in directia
dk sa
conduca la descresterea maxima a functiei
F(x).
Pentru determinarea valorii optime a coeficientului
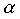 k
k,
functia
F(x) calculata in noua aproximatie
xk+1 se exprima
ca o functie de
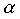 k
k:
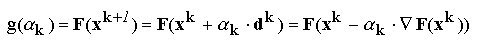
sau:
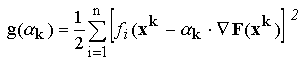
Daca se admite ca factorul
 k
k
are valori suficient de mici, pentru a putea neglija puterile sale superioare lui 1,
functiile
fi pot fi dezvoltate in serii Taylor in jurul
punctului
xk, neglijand toti termenii neliniari:
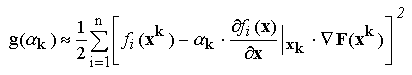
sau:
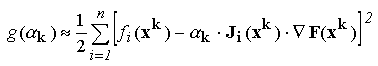
Functia
F(xk+1) va atinge valoarea minima
in acel punct
xk+1 pentru care are loc anularea derivatei
functiei
g in raport cu
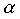 k
k :
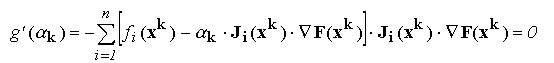
Solutia acestei ecuatii este :
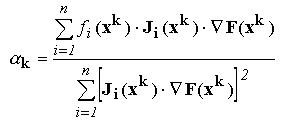
Aceasta relatie mai poate fi scrisa sub forma condensata:
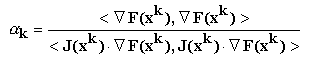
unde parantezele unghiulare indica produsul scalar a doi vectori.
Pe baza relatiilor de mai sus se poate defini urmatoarea schema de aplicare a
metodei gradientului:
Schema de aplicare a metodei gradientului
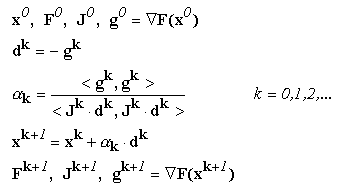
In aceste relatii expresia coeficientului
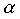 k
k
este diferita, dar echivalenta cu cea stabilita anterior. La numitor, gradientul
gk a fost inlocuit cu directia de deplasare
dk,
pentru a permite efectuarea unei comparatii intre metoda gradientului si metoda
gradientului conjugat ce va fi prezentata mai jos.
Se constata ca, in comparatie cu metodele de tip Newton,
metoda gradientului nu necesita inversarea matricei Jacobian si nici rezolvarea
unui sistem de ecuatii liniare, insa presupune efectuarea unui numar sporit de
inmultiri matriceale, legate de stabilirea valorii optime a coeficientului
 k
k.
Metoda gradientului conjugat
Algoritmul acestei metode este foarte asemanator cu cel prezentat
pentru metoda gradientului simplu. De aceasta data, insa, la o iteratie
k,
directia de deplasare
dk se determina ca o combinatie liniara
dintre gradientul
gk luat cu semn schimbat si directia de
deplasare din iteratia anterioara:
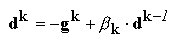
unde coeficientul
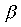 k
k
are expresia:
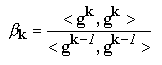
In aceste conditii, schema de aplicare a metodei gradientului conjugat este urmatoarea:
Schema de aplicare a metodei gradientului conjugat
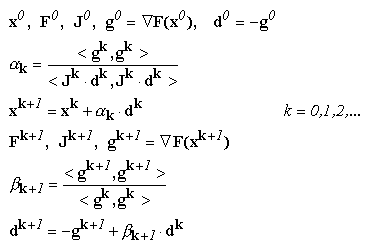
Se constata ca pentru prima iteratie nu se poate calcula un
coeficient
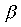 k
k,
astfel incat pornirea algoritmului se face conform metodei gradientului, pentru
care se alege
d0 = - g0.
Pentru detalii suplimenatare privind
rezolvarea sistemelor de ecuatii neliniare, se poate consulta cartea
"Calcul numeric cu aplicatii in Turbo Pascal".
 Aplicatii - Lista lucrarilor de laborator
Aplicatii - Lista lucrarilor de laborator