Lucrarea 6. Rezolvarea sistemelor de ecuatii liniare cu metode iterative: metodele Jacobi, Seidel-Gauss si suprarelaxarii succesive
Tema A - Metoda iterativa
Jacobi
Tema B - Metoda iterativa Seidel-Gauss
Tema C - Metoda suprarelaxarii succesive
Determinarea solutiei exacte a sistemului A * x = b cu ajutorul
unor metode de tip iterativ este posibila numai dupa efectuarea unui numar
nelimitat
- teoretic infinit - de iteratii sau pasi. Deoarece nici o metoda
practica nu poate cicla la infinit, rezulta ca metodele iterative determina
doar o solutie aproximativa, aproximare prin trunchiere, care se
abate mai mult sau mai putin fata de solutia exacta x*, in functie
de precizia de calcul dorita.
Mai concret, metodele iterative apeleaza la construirea unui sir de aproximatii
succesive x_0, x_1, ... , x_k care, in anumite conditii, tinde catre
solutia exacta x*. In cazul in care pentru sirul aproximatiilor
succesive nu este posibila definirea unei limite, se spune ca metoda respectiva
diverge.
In cazul in care sirul aproximatiilor succesive are o limita, se spune
ca metoda este convergenta. In acest caz se poate defini o relatie de recurenta
intre doua aproximatii succesive x_k si x_(k+1). Definirea
relatiei de recurenta intre aproximatiile succesive se face pornind de
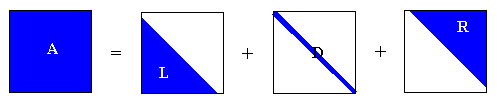
la desfacerea matricei A in alte doua matrice:
In general, toate metodele iterative de rezolvare a sistemelor de ecuatii liniare, definesc matricele N si P din desfacerea A = N - P pornind de la desfacerea standard a matricei A:
Tema A - Metoda iterativa Jacobi
Metoda iterativa Jacobi, numita si metoda iteratiilor simultane,
foloseste o desfacere A = N - P, in care matricele N si P
se aleg conform relatiei:
unde D, L si R sunt matricele din desfacerea standard, iar toate elementele diagonale a_ii sunt nenule. Folosind aceasta desfacere in relatia generala de recurenta, se obtine forma matriceala a relatiei de recurenta pentru metoda Jacobi:
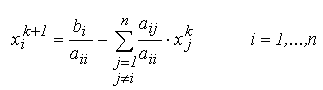
Metoda iterativa Jacobi este convergenta daca, pentru fiecare linie din matricea A, suma valorilor absolute ale termenilor din afara diagonalei principale nu depaseste valoarea absoluta a termenului diagonal. Matricele care satisfac aceasta proprietate se numesc diagonal dominante.
O particularitate a metodei Jacobi se refera la modul cum este folosita aproximatia anterioara x_k pentru calculul noii aproximatii x_(k+1). Astfel, se constata ca noile aproximatii ale fiecarei necunoscute
Algoritmul 1 - Sisteme de ecuatii liniare - Metoda iterativa Jacobi
- Definirea sistemului de ecuatii: rangul n, matricea coeficientilor A, vectorul termenilor liberi b;
- Definirea parametrilor de iterare: abaterea relativa maxima admisa Emax si numarul maxim de iteratii Nmax;
- Calcul iterativ:
- Stabilirea aproximatiei initiale, identica cu termenii liberi:
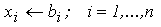
- Initializarea procesului iterativ: It <-- 0.
- Initializarea abaterii relative maxime in iteratia curenta cu o valoare superioara lui Emax : Dx <-- Emax + 1.
- Daca s-a atins numarul maxim de iteratii (It=Nmax) sau abaterea Dx a trecut sub valoarea admisa ( Dx <= Emax ), se incheie procesul iterativ si se trece la pasul 4;
- Trecerea la o noua iteratie: It <-- It + 1.
- Calculul noii aproximatii in vectorul y:
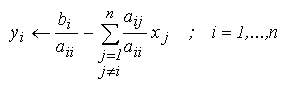
- Calculul abaterii relative maxime in iteratia curenta:
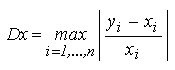
- Actualizarea vectorului aproximatiilor din ultima iteratie:
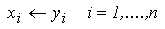
- Se revine la pasul 3.iv.
- Stabilirea aproximatiei initiale, identica cu termenii liberi:
- Stabilirea conditiilor de iesire din bucla iterativa:
- daca Dx <= Emax (metoda converge), se afiseaza solutia
aproximativa
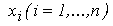 si
numarul de iteratii efectuate It;
si
numarul de iteratii efectuate It; - daca Dx>Emax, dar It=Nmax (metoda nu converge), se afiseaza mesajul "Depasire numar maxim iteratii";
- daca Dx <= Emax (metoda converge), se afiseaza solutia
aproximativa
Tema B - Metoda iterativa Seidel-Gauss
Metoda iterativa Seidel - Gauss, numita si metoda iteratiilor succesive, foloseste o desfacere A = N - P, in care matricele N si P se aleg conform relatiei:
P = - R
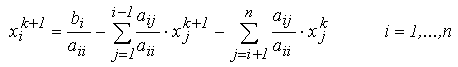
O comparatie intre formulele de iterare ale metodelor Jacobi si Seidel - Gauss evidentiaza urmatoarea particularitate:
- in cazul metodei Jacobi noile aproximatii se determina folosind exclusiv aproximatiile din iteratia anterioara;
-
prin contrast, metoda Seidel-Gauss
calculeaza noile aproximatii
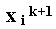 folosind
si aproximatiile determinate deja in iteratia curenta
(
folosind
si aproximatiile determinate deja in iteratia curenta
(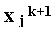 ,
j=1,...,i-1 ).
,
j=1,...,i-1 ).
O alta consecinta a utilizarii aproximatiilor deja calculate pentru determinarea celorlalte aproximatii se refera la convergenta metodei. De regula, metoda Seidel - Gauss aduce un plus de viteza de convergenta fata de metoda Jacobi. Astfel, este de asteptat ca, pornind de la o aceeasi aproximatie initiala, metoda Seidel - Gauss sa asigure precizia impusa intr-un numar mai mic de iteratii.
Ca si in cazul metodei Jacobi, conditia de convergenta a metodei Seidel - Gauss o reprezinta forma diagonal dominanta a matricei coeficientilor A.
Algoritmul 2 - Sisteme de ecuatii liniare - Metoda iterativa Seidel-Gauss
- Definirea sistemului de ecuatii: rangul n, matricea coeficientilor A, vectorul termenilor liberi b;
- Definirea parametrilor de iterare: abaterea relativa maxima admisa Emax si numarul maxim de iteratii Nmax;
- Calcul iterativ:
- Stabilirea aproximatiei initiale, identica cu termenii liberi:
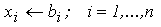
- Initializarea procesului iterativ: It <-- 0.
- Initializarea abaterii relative maxime in iteratia curenta cu o valoare superioara lui Emax : Dx <-- Emax + 1.
- Daca s-a atins numarul maxim de iteratii (It=Nmax) sau abaterea Dx a trecut sub valoarea admisa ( Dx <= Emax ), se incheie procesul iterativ si se trece la pasul 4;
- Trecerea la o noua iteratie: It <-- It + 1.
- Initializarea abaterii relative maxime in iteratia curenta : Dx <-- 0;
- Calculul noii aproximatii si al abaterii relative maxime folosind
o variabila tampon z:
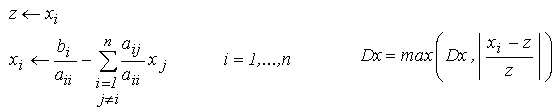
- Se revine la pasul 3.iv.
- Stabilirea aproximatiei initiale, identica cu termenii liberi:
- Stabilirea conditiilor de iesire din bucla iterativa:
- daca Dx <= Emax (metoda converge), se afiseaza solutia
aproximativa
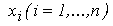 si
numarul de iteratii efectuate It;
si
numarul de iteratii efectuate It; - daca Dx>Emax, dar It=Nmax (metoda nu converge), se afiseaza mesajul "Depasire numar maxim iteratii";
- daca Dx <= Emax (metoda converge), se afiseaza solutia
aproximativa
Tema C - Metoda suprarelaxarii succesive
Metoda suprarelaxarii succesive este o varianta modificata a metodei
iterative Seidel - Gauss, care urmareste accelerarea suplimentara a convergentei
procesului iterativ. In acest scop, se utilizeaza o desfacere A = N
- P care depinde de un parametru real![]() ,
denumit parametru de accelerare (relaxare):
,
denumit parametru de accelerare (relaxare):
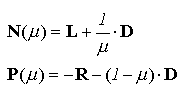
Introducerea matricelor N(
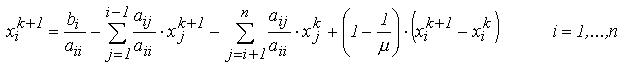
Pe de alta parte, se constata ca metoda suprarelaxarii succesive nu poate folosi direct formula de iterare, deoarece aceasta determina aproximatia
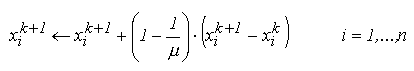
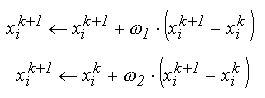

-
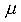 =1,
=1,
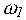 =0,
=0,
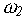 =1.
Aproximatiei nou calculate nu i se aplica nici o corectie. Se obtine metoda
Seidel - Gauss obisnuita;
=1.
Aproximatiei nou calculate nu i se aplica nici o corectie. Se obtine metoda
Seidel - Gauss obisnuita; -
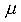 =1/2,
=1/2,
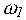 =-1,
=-1,
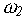 =0 .
Aproximatia nou calculata coincide cu aproximatia din iteratia anterioara.
Procesul este stationar, toate aproximatiile ramanand identice cu aproximatia
initiala.
=0 .
Aproximatia nou calculata coincide cu aproximatia din iteratia anterioara.
Procesul este stationar, toate aproximatiile ramanand identice cu aproximatia
initiala.
In general, valori ale parametrului de accelerare 1 <
Algoritmul 3 - Sisteme de ecuatii liniare - Metoda suprarelaxarii succesive
- Definirea sistemului de ecuatii: rangul n, matricea coeficientilor A, vectorul termenilor liberi b;
- Definirea parametrilor de iterare: abaterea relativa maxima admisa Emax si numarul maxim de iteratii Nmax;
- Calcul iterativ:
- Stabilirea aproximatiei initiale, identica cu termenii liberi:
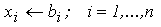
- Initializarea procesului iterativ: It <-- 0.
- Initializarea abaterii relative maxime in iteratia curenta cu o valoare superioara lui Emax : Dx <-- Emax + 1.
- Daca s-a atins numarul maxim de iteratii (It=Nmax) sau abaterea Dx a trecut sub valoarea admisa ( Dx <= Emax ), se incheie procesul iterativ si se trece la pasul 4;
- Trecerea la o noua iteratie: It <-- It + 1.
- Initializarea abaterii relative maxime in iteratia curenta : Dx <-- 0;
- Calculul noii aproximatii si al abaterii relative maxime folosind
o variabila tampon z:
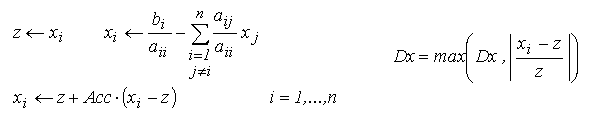
- Se revine la pasul 3.iv.
- Stabilirea aproximatiei initiale, identica cu termenii liberi:
- Stabilirea conditiilor de iesire din bucla iterativa:
- daca Dx <= Emax (metoda converge), se afiseaza solutia
aproximativa
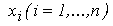 si
numarul de iteratii efectuate It;
si
numarul de iteratii efectuate It; - daca Dx>Emax, dar It=Nmax (metoda nu converge), se afiseaza mesajul "Depasire numar maxim iteratii";
- daca Dx <= Emax (metoda converge), se afiseaza solutia
aproximativa
Pentru detalii suplimenatare privind
metodele iterative si convergenta procesului iterativ, se poate consulta
cartea
"Calcul numeric cu aplicatii in Turbo Pascal".