Lucrarea 9.
Ecuatii neliniare: accelerarea convergentei metodelor de ordin I - Metoda
falsei pozitii si metoda Aitken
In aplicatiile practice intereseaza, desigur,
asigurarea unei convergente cat
mai rapide a procesului iterativ care construieste sirul aproximatiilor succesive.
In limbajul calculului numeric, accelerarea convergentei inseamna aplicarea unor metode
cu ordin de convergenta cat mai mare. Dintre metodele prezentate in paragrafele
anterioare, cele mai bune performante din acest punct de vedere le are metoda Newton,
caracterizata de convergenta patratica. Metodele de partitionare (metodele
bisectiei,
a secantei
sau a cautarii cu pas variabil) sau metoda contractiei intra in categoria
metodelor de ordin I. Diferitele variante ale metodei Newton se caracterizeaza,
in general, prin reducerea ratei de convergenta: metoda Traub asigura doar o
convergenta superliniara, in timp ce metoda Newton simplificata coboara pana la
convergenta liniara. Exceptia o reprezinta metoda Bailey, care folosind si derivata
de ordin doi calculata analitic, ajunge la o convergenta superpatratica, fara a atinge
insa ordinul III. Mai trebuie spus ca, de regula, cresterea ordinului de convergenta
este insotita de amplificarea volumului de calcule efectuate la fiecare iteratie.
Daca vrem ca metoda folosita sa fie eficienta din punct de vedere numeric trebuie
sa mentinem aceasta balanta cat mai aproape de echilibru. In fond, interesul final
este un timp de calcul cat mai redus, adica un numar mic de iteratii, dar si un timp
de calcul pe iteratie redus.
Tema A - Metoda falsei pozitii
Metoda falsei pozitii reprezinta un caz particular
al metodei Newton. Ca procedeu de accelerare, ea nu trebuie raportata insa la
metoda Newton, pe care dealtfel o "franeaza", ci la metodele de ordin intai,
fata de care ofera convergenta superliniara. Modelul matematic porneste de la
formula de iterare a metodei Newton:
Tema A - Metoda falsei pozitii
<----------- algoritm
Tema B - Metoda Aitken
<----------- algoritm
Dintre procedeele de accelerare a convergentei
cunoscute, in cele ce urmeaza vom descrie succint metoda falsei pozitii si metoda Aitken.
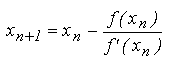
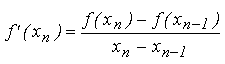
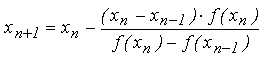
 Metodei falsei pozitii i se poate asocia o
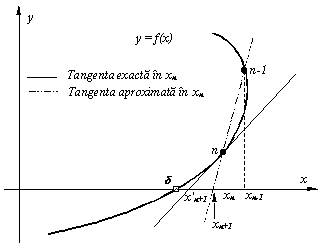
interpretare geometrica care face mai "transparent" suportul matematic descris.
Astfel (vezi figura alaturata), pornind de la aproximatiile x_n si x_n-1,
tangenta in punctul x_n este aproximata prin dreapta ce trece prin punctele n-1
si n, iar noua aproximatie x_n+1 corespunde intersectiei acestei drepte cu axa
absciselor. In figura se indica si o comparatie intre metoda Newton si metoda
falsei pozitii, sugerandu-ne si raspunsul la intrebarea: cat de mult se abate
x_n+1 fata de x'_n+1 (aproximatia calculata cu formula Newton) ? Cu cat curbura
functiei f(x) intre punctele n-1 si n este mai mare, cu atat aproximatia x_n+1
se va abate mai mult fata de valoarea calculata cu formula de iterare a metodei
Newton. Altfel spus, rata de convergenta a metodei falsei pozitii este cu atat
mai mare cu cat, in aproximatia curenta x_n, functia f(x) are o derivata de
ordin doi f"(x_n) mai mica in valoare absoluta.
Metodei falsei pozitii i se poate asocia o
interpretare geometrica care face mai "transparent" suportul matematic descris.
Astfel (vezi figura alaturata), pornind de la aproximatiile x_n si x_n-1,
tangenta in punctul x_n este aproximata prin dreapta ce trece prin punctele n-1
si n, iar noua aproximatie x_n+1 corespunde intersectiei acestei drepte cu axa
absciselor. In figura se indica si o comparatie intre metoda Newton si metoda
falsei pozitii, sugerandu-ne si raspunsul la intrebarea: cat de mult se abate
x_n+1 fata de x'_n+1 (aproximatia calculata cu formula Newton) ? Cu cat curbura
functiei f(x) intre punctele n-1 si n este mai mare, cu atat aproximatia x_n+1
se va abate mai mult fata de valoarea calculata cu formula de iterare a metodei
Newton. Altfel spus, rata de convergenta a metodei falsei pozitii este cu atat
mai mare cu cat, in aproximatia curenta x_n, functia f(x) are o derivata de
ordin doi f"(x_n) mai mica in valoare absoluta.
Daca se compara formulele de iterare ale metodelor falsei pozitii si secantei se constata ca se obtin forme similare. Echivalenta celor doua metode este insa numai aparenta: formulele de iterare sunt aceleasi, dar ele se aplica unor puncte diferite de pe curba y=f(x). Metoda falsei pozitii foloseste permanent ultimele doua aproximatii, pe cand metoda secantei, datorita conditiei de incadrare a solutiei exacte, poate impune "uitarea" unor puncte "noi" si inlocuirea lor cu puncte "vechi". In aceasta consta, de fapt, deosebirea esentiala intre cele doua metode si, tot de aici, rezulta proprietatile superioare de convergenta ale metodei falsei pozitii. In timp ce metoda secantei converge liniar, metoda falsei pozitii are o convergenta superliniara; se poate arata ca ordinul acestei metode este
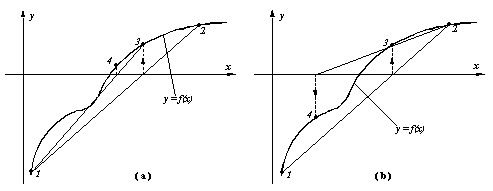
O ultima observatie care se impune a fi facuta asupra utilizarii metodei falsei pozitii revine la formula de iterare. Fiind vorba de o formula de iterare de ordin superior unitatii, aplicarea ei necesita folosirea unei metode cu "autopornire" care, pe langa aproximatia initiala x_0, sa puna la dispozitie o aproximatie suplimentara x_1, necesara pentru determinarea lui x_2. Pentru primul pas se poate utiliza orice metoda cu ordin de convergenta inferior, de exemplu metoda secantei. Primul punct intermediar x3 se determina dupa metoda secantei, iar in interiorul buclei iterative aproximatiile succesive se calculeaza folosind direct formula de iterare a metodei falsei pozitii.
Algoritmul 1 - Ecuatii neliniare - Metoda falsei pozitii
- Definirea functiei f(x) si a functiei g(x), ultima fiind folosita de catre metoda de pornire.
- Definirea preciziei de calcul dorite Eps
- Initializarea contorului de iteratii (It <--- 0) si a aproximatiei initiale x(0)
- Pornirea algoritmului folosind o metoda de ordin I : x(1) <--- g(x(0))
-
Aplicarea metodei falsei pozitii:
- Trecerea la o noua iteratie: It <--- It+1
-
Calculul noii aproximatii:
x(It+1) = ( x(It-1)*f(x(It)) - x(It)*f(x(It-1)) ) / ( f(x(It)) - f(x(It-1)) ) -
Verificarea conditiei de oprire:
- Daca | x(It+1) - x(It) | < Eps, precizia impusa a fost atinsa si se trece la pasul 6.
- Daca | x(It+1) - x(It) | > Eps, procesul iterativ continua prin revenirea la pasul 5.i.
- Radacina aproximativa este x(It+1).
Metoda Aitken porneste de la un sir de aproximatii succesive { x_n } convergent liniar si construieste un sir { x'_n } convergent patratic. In principiu, accelerarea Aitken poate fi aplicata oricarui sir de aproximatii generat cu o metoda de ordin I. In continuare vom considera insa o metoda de contractie, ce foloseste formula generala de iterare:
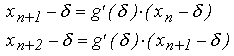
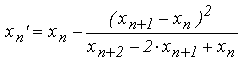
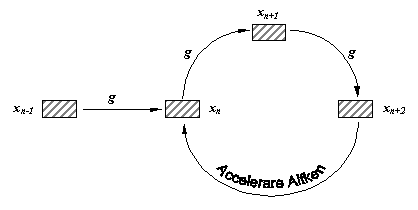
Principiul accelerarii Aitken. Pornind de la o aproximatie x_n-1, se determina aproximatia x_n, folosind o metoda de ordin unu, dupa care se intra in bucla de accelerare. Se aplica mai intai doi pasi de ordin unu, pentru calculul aproximatiilor x_n+1 si x_n+2, dupa care se recalculeaza x_n, folosind accelerarea Aitken. Bucla se reia pana la satisfacerea unui criteriu de oprire.
Algoritmul 2 - Ecuatii neliniare - Metoda Aitken
- Definirea functiei g(x), si a preciziei de calcul dorite Eps.
- Definirea rangului de la care incolo se aplica accelerarea ( r > 0 ).
- Initializarea contorului de iteratii (It <--- 0) si a aproximatiei initiale x(0)
-
Calculul aproximatiilor succesive pana la rangul r+2.
- Trecerea la o noua iteratie : It <--- It+1
- Calculul noii aproximatii : x(It) = g(x(It-1))
-
Controlul incheierii algoritmului de pornire:
- Daca It < r+2 se revine la pasul 4.i.
- Daca It = r+2, algoritmul de pornire se incheie si se trece la pasul 5.
-
Aplicarea accelerarii Aitken:
-
Accelerarea cu formula Aitken :
x(r) = x(r) - ( x(r+1) - x(r) )^2 / ( x(r+2) - 2*x(r+1) + x(r) ) -
Recalcularea aproximatiilor de rang r+1 si r+2:
x(r+1) = g(x(r)) x(r+2) = g(x(r+1)) -
Verificarea conditiei de oprire:
- Daca | x(r+2) - x(r+1) | < Eps, precizia impusa a fost atinsa si se trece la pasul 6.
- Daca | x(r+2) - x(r+1) | > Eps, procesul iterativ continua prin revenirea la pasul 5.i.
-
Accelerarea cu formula Aitken :
- Radacina aproximativa este x(r+2)
Pentru detalii suplimenatare privind
procedeele de accelerare a convergentei metodelor iterative de rezolvare a
ecuatiilor neliniare, se poate consulta cartea
"Calcul numeric cu aplicatii in Turbo Pascal".